《实用非参数统计》课程教学资源（阅读材料）Permutation test

Bootstrap,Jackknife and other resampling methods Part V:Permutation tests Rozenn Dahyot Room 128,Department of Statistics Trinity College Dublin,Ireland dahyot mee.tcd.ie 2005 R.Dahyot (TCD) 453 Modern statistical methods 20051/22

Bootstrap, Jackknife and other resampling methods Part V: Permutation tests Rozenn Dahyot Room 128, Department of Statistics Trinity College Dublin, Ireland dahyot@mee.tcd.ie 2005 R. Dahyot (TCD) 453 Modern statistical methods 2005 1 / 22

So far The resampling methods are: o Bootstrap resampling:generate samples with the same size n as x with replacement. Jackknife subsampling generate samples with a smaller size than x without replacement. Used for: Compute accuracy measures (standard error,bias,etc.)of a statistic 0 from one set x (x1,...,xn). oCompare two sets of observations:the example of the mouse data R.Dahyot (TCD) 453 Modern statistical methods 20052/22

So far The resampling methods are: Bootstrap resampling: generate samples with the same size n as x with replacement. Jackknife subsampling : generate samples with a smaller size than x without replacement. Used for: Compute accuracy measures (standard error, bias, etc.) of a statistic θˆ from one set x = (x1, · · · , xn). Compare two sets of observations: the example of the mouse data R. Dahyot (TCD) 453 Modern statistical methods 2005 2 / 22

Example on the mouse data Data (Treatment group) 94;197:16;38;99:141;23 Data(Control group) 52;104;146;10:51;30:40;27:46 Table:The mouse data [Efron].16 mice divided assigned to a treatment group (7)or a control group(9).Survival in days following a test surgery.Did the treatment prolong survival R.Dahyot (TCD) 453 Modem statistical methods 20053/22

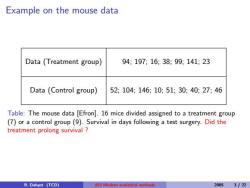
Example on the mouse data Data (Treatment group) 94; 197; 16; 38; 99; 141; 23 Data (Control group) 52; 104; 146; 10; 51; 30; 40; 27; 46 Table: The mouse data [Efron]. 16 mice divided assigned to a treatment group (7) or a control group (9). Survival in days following a test surgery. Did the treatment prolong survival ? R. Dahyot (TCD) 453 Modern statistical methods 2005 3 / 22

Example on the mouse data Compute B bootstrap samples for each group ·x8=(x81…,x8) *(b) x=(…,温g) B bootstrap replications are computed:(= you can approximate the p.d.f.of the replications by a histogram. R.Dahyot (TCD) 453 Modern statistical methods 20054/22

Example on the mouse data 1 Compute B bootstrap samples for each group I x ∗(b) Treat = (x ∗(b) Treat 1 , · · · , x ∗(b) Treat 7 ) I x ∗(b) Cont = (x ∗(b) Cont 1 , · · · , x ∗(b) Cont 9 ) 2 B bootstrap replications are computed: θˆ∗ (b) = x ∗(b) Treat − x ∗(b) Cont 3 you can approximate the p.d.f. of the replications by a histogram. R. Dahyot (TCD) 453 Modern statistical methods 2005 4 / 22

Example on the mouse data 003 0.05 P(0*) 0.04 0.03 0.02 0,01 -100 00 150 200 Figure:P.d.f.P()(histogram)of the replication (=30.63 and 5seB=26.85). R.Dahyot (TCD) 453 Modem statistical methods 2005 5/22

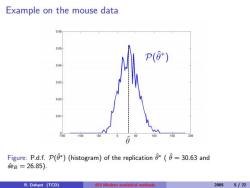
Example on the mouse data Figure: P.d.f. P(θˆ∗ ) (histogram) of the replication θˆ∗ ( θˆ = 30.63 and seˆ B = 26.85). R. Dahyot (TCD) 453 Modern statistical methods 2005 5 / 22

Introduction oTwo sample problem definitions Parametric solution Non parametric solution: permutation test randomization test bootstrap test R.Dahyot (TCD) 453 Modern statistical methods 20056/22

Introduction Two sample problem : definitions Parametric solution Non parametric solution: I permutation test I randomization test I bootstrap test R. Dahyot (TCD) 453 Modern statistical methods 2005 6 / 22

The two sample problem Two independent random sample are observed xa and xb drawn from possibly different probability density functions: Fgxa={x,1,…,X,n} Fbxb={xb,1,…,b,m} Definition The null hypothesis Hto assumes that there is no difference in between the density function Fa=Fb. R.Dahyot (TCD) 453 Moder statistical methods 20057/22

The two sample problem Two independent random sample are observed xa and xb drawn from possibly different probability density functions: Fa xa = {xa,1, · · · , xa,n} Fb xb = {xb,1, · · · , xb,m} Definition The null hypothesis H0 assumes that there is no difference in between the density function Fa = Fb. R. Dahyot (TCD) 453 Modern statistical methods 2005 7 / 22

Hypothesis test and Achieved significance level (ASL) Definition A hypothesis test is a way of deciding whether or not the data decisively reject the hypothesis Ho. Definition The achieved significance level of the test (ASL)is defined as: AsL=P(0*≥Ho) =6P(1to)d0 The smaller ASL,the stronger is the evidence of Ho false.The notation star differentiates between an hypothetical value generated according to Ho,and the actual observation 0. R.Dahyot (TCD)】 453 Modem statistical methods 2005 8/22

Hypothesis test and Achieved significance level (ASL) Definition A hypothesis test is a way of deciding whether or not the data decisively reject the hypothesis H0. Definition The achieved significance level of the test (ASL) is defined as: ASL = P(θ ˆ∗ ≥ θ ˆ|H0) = R +∞ θˆ P(θˆ∗ |H0) dθˆ∗ The smaller ASL, the stronger is the evidence of H0 false. The notation star differentiates between an hypothetical value θˆ∗ generated according to H0, and the actual observation θˆ. R. Dahyot (TCD) 453 Modern statistical methods 2005 8 / 22

Parametric test o A tradionnal way is to consider some hypotheses:Fa~N(ua,2) and F~N(ub,2),and the null hypothesis becomes ua =ub. Under Ho,the statistic =Xa-can be modelled as a normal distribution with mean 0 and variance2(). o The ASL is then computed: -(*-2 ∫+心e2 ASL= d0* √2π0a R.Dahyot (TCD) 453 Modern statistical methods 20059/22

Parametric test A tradionnal way is to consider some hypotheses: Fa ∼ N (µa, σ2 ) and Fb ∼ N (µb, σ2 ), and the null hypothesis becomes µa = µb. Under H0, the statistic θˆ = xa − xb can be modelled as a normal distribution with mean 0 and variance σ 2 θˆ = σ 2 ( 1 m + 1 n ). The ASL is then computed: ASL = Z +∞ θˆ e −(θˆ∗−θˆ) 2 2σ2 θˆ √ 2πσθˆ dθˆ∗ R. Dahyot (TCD) 453 Modern statistical methods 2005 9 / 22

Parametric test oo is unknown and has to be estimated from the data: a2=∑1=(xai-x,)2+∑1(xb1-xb2 m+n-2 For the mouse data ASL =.131 the null hypothesis cannot be rejected. o However,this(parametric)method relies on the hypotheses made while calculating the ASL. R.Dahyot (TCD) 453 Modern statistical methods 2005 10/22

Parametric test σ is unknown and has to be estimated from the data: σ 2 = Pn i=1(xai − xa) 2 + Pm i=1(xbi − xb) 2 m + n − 2 For the mouse data ASL = .131 : the null hypothesis cannot be rejected. However, this (parametric) method relies on the hypotheses made while calculating the ASL. R. Dahyot (TCD) 453 Modern statistical methods 2005 10 / 22