《经济数学》课程教学课件（PPT讲稿）第一章 函数与极限 1-4 无穷大与无穷小

第四节无穷小与无穷大 二无穷小 二、无穷大 三、无穷小与无穷大的关系

第四节 无穷小与无穷大 二、 无穷大 三 、 无穷小与无穷大的关系 一、 无穷小

一、无穷小 定义、若x→x(或x→∞)时，函数f(x)→0， 则称函数f(x(或x→∞为x→xo时的无穷小 例如： 1im(x-1)=0,函数x-1当x→1时为无穷小 x>1 1im=0,函数当x→o时为无穷小， x→0X lim =0,函数 一当x→-0时为无穷小

一、 无穷小 当 定义、 若 时 , 函数 则称函数 例如 : 函数 当 时为无穷小; 函数 时为无穷小; 函数 当 (或x → ) 为 时的无穷小 . 时为无穷小. (或x → )

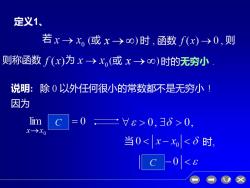
定义1、 若x→x,或x→o0)时，函数f(x)→0，则 则称函数f(x)为x→x,(或x→o)时的无穷小 说明：除0以外任何很小的常数都不是无穷小1 因为 lim C=0=16>0,38>0, 当0<x-x<8时 C-0<

定义1、 说明: 除 0 以外任何很小的常数都不是无穷小 ! 因为 当 时, C C (或 x → ) 时 , 函数 则称函数 为 若 (或 x → ) 则 时的无穷小

定理1（无穷小与函数极限的关系) lim f(x)=A 三f(x)=A+a,其中a为x→x。 x→x0 时的无穷小量 证： lim f(x)=4 x→X0 V>0,3δ>0，当0<x-x0<6时有 f(x)-A<8 a=x)-⊥ lim a=0 x→Xo 对自变量的其它变化过程类似可证

定理 1 ( 无穷小与函数极限的关系 ) 其中 为 0 x → x 时的无穷小量 . f x A x x = → lim ( ) 0 f (x) = A+ , 证: f x A x x = → lim ( ) 0   0,   0, 当 0  x − x0   时,有 f (x) − A    = f (x) − A lim 0 0 = →  x x 对自变量的其它变化过程类似可证

二、无穷大 定义2.若任给M>0,总存在6>0正数X),使对 一切满足不等式0X)的x,总有 f(x)>M ① 则称函数f(x)当x→x(x>∞)时为无穷大，记作 lim f(x)=co. (limf(x)=∞) x→xo X-→00 若在定义中将①式改为f(x)>M(f(x)<-M) 则记作1imf(x)=+oo(limf(x)=-o》 x→X0 x→X0 (x→0) (x→0

二、 无穷大 定义2 . 若任给 M > 0 , 一切满足不等式 的 x , 总有 则称函数 当 时为无穷大, 使对 若在定义中将 ①式改为 ① 则记作 ( lim ( ) ) ( ) 0 = − → → f x x x x ( x  X ) ( x → ) (lim ( ) =  ) → f x x (正数 X ) , 记作 ( f (x)  −M ), 总存在

例、证明1im- =00 x>1x-1 证：任给正数M,要使 ,即-1 只要取δ=1 则对满足0M 所以1im x→1x-1 说明：若1imf(x)=0,则直线x=x0 xx0 为曲线y=∫(x)的铅直近线 渐近线

例 、证明 证: 任给正数 M , 要使 即 只要取 , 1 M  = 则对满足 的一切 x , 有 所以 若 则直线 0 x =x 为曲线 的铅直渐近线 . 说明: 渐近线

无穷小与无穷大的关系 定理2.在自变量的同一变化过程中 若f(x)为无穷大，则 为无穷小 f(x 若f(x)为无穷小，且f(x)≠0，则 为无穷大 说明：据此定理，关于无穷大的问题都可转化为 无穷小来讨论：

无穷小与无穷大的关系 若 为无穷大, ( ) 1 f x 为无穷小 ; 若 为无穷小, 且 f (x)  0, 则 ( ) 1 f x 为无穷大. 则 据此定理 , 关于无穷大的问题都可转化为 无穷小来讨论. 定理2. 在自变量的同一变化过程中, 说明:

内容小结 1.无穷小与无穷大的定义 2.无穷小与函数极限的关系 3.无穷小与无穷大的关系

内容小结 1. 无穷小与无穷大的定义 2. 无穷小与函数极限的关系 3. 无穷小与无穷大的关系