吉林大学：《计算机图形学》课程电子教案（PPT课件）第四章 曲线和曲面 第五节 B样条曲线和曲面

第五节B样条曲线和曲面 B样条曲线 给定nt1个控制点Po,P1,,Pn,它 们所确定的阶B样条曲线是： P(u)=∑Nk(u)R i=0 其中W,k(ω递归定义如下：

第五节 B样条曲线和曲面 B样条曲线 给定n+1个控制点P0，P1，…，Pn，它 们所确定的k阶B样条曲线是：  = =  n i 0 i (u)P i ,k P(u) N 其中Ni，k (u)递归定义如下：

%,不@，40 0sjzn+k-1 0,其它 ,k(u以4 k-o4u Ui+k-1-u; +ku+1 +1k-1《u), k>1,0si≤n 这里，凸，…，“n*,是一个非递减的 序列，称为节点，（，，。，“称为 节点向量。定义中可能出现。，氵 这时约定 为0

这里u0，u1，…，un+k，是一个非递减的 序列，称为节点，(u0，u1，…，un+k )称为 节点向量。定义中可能出现 ，这时约定 为0。             + − + − + − + + − − + − − =      + − +   = k 1,0 i n (u), i 1 ,k 1 N i 1 u i k u u i k u (u) i ,k 1 N i u i k 1 u i u u (u) i ,k N 0 , 其 它 , 0 i n k 1 i 1 u u i 1 ， u (u) i,1 N 0 0

选取，F2,k=1,控制顶点是P,P1,P2, 这样应选择参数节点什k件1=4个，设节点向 量是(46，“，，)，按式定义，可写出 三个基函数： 1，u0≤u≤u1 u)=o, u1≤u≤u2 0,u2≤u≤u3 6o uo≤u≤u1 u1≤u≤u2 ≤u≤u3 w-8 u0≤u≤u1 N2. 1≤u≤u2 , u2 ,≤u≤u3

选取，n=2，k=1，控制顶点是P0，P1，P2， 这样应选择参数节点n+k+1=4个，设节点向 量是(u0，u1，u2，u3 )，按式定义，可写出 三个基函数：            =            =            = 3 u u 2 1 , u 2 u u 1 0 , u 1 u u 0 0 , u (u) 2,1 N 3 u u 2 0 , u 2 u u 1 1 , u 1 u u 0 0 , u (u) 1,1 N 3 u u 2 0 , u 2 u u 1 0 , u 1 u u 0 1 , u (u) 0,1 N

由公式可知所定义的B样条曲线是 P (U)=NO.P+N u+N2)P P0:u0≤uu1 P1u1u≤u2 P2 u2u≤u3

由公式可知所定义的B样条曲线是            = = + + 3 u u 2 , u 2 P 2 u u 1 , u 1 P 1 u u 0 , u 0 P 2 (u)P 2,1 N 1 (u)P 1,1 N 0 (u)P 0,1 P(u) N

选取3，仁2，于是有四个控制顶点P? P1,P2:P3应有参数节点tk41=6个，.设节 点向量是0,0,1,2,3,3)，试画出所确 定的2阶B样条曲线。 取0.5，进行计算。因为0.5∈[0,1]=[w, 山2]，因此%1(0.5)=1，而其它的W.1(0.5)=0, ≠1。往下用公式做递归计算。 0.20.5)= 0.5- 1-0.51=0.5 0-0 .0 1-0 N120.5)= 0.5-0 2-0.5.0=0.5 1-0 2-1

选取n=3，k=2，于是有四个控制顶点P0， P1，P2，P3，应有参数节点n+k+1=6个，设节 点向量是(0，0，1，2，3，3)，试画出所确 定的2阶B样条曲线。 取u=0.5，进行计算。因为0.5∈[0，1]=[u1， u2 ]，因此N1,1(0.5)=1，而其它的Ni,1(0.5)=0， i≠1。往下用公式做递归计算。 0 0.5 2 1 2 0.5 1 1 0 0.5 0 (0.5) 1,2 N 1 0.5 1 0 1 0.5 0 0 0 0.5 0 (0.5) 0,2 N  = − −  + − − =  = − −  + − − =

%2(0.5)和%.2(0.5)，不必计算，因为 计算它们需要的D2时的W,1(0.5)=0, 所以知%，2(0.5)=%2(0.5)=0。这样代 入公式计算P(0.5),有： P(0.5)=N0,20.5)P0+N,20.5)P +N2,20.5》P2+N3,20.5》P3 =0.5-(o+P1)

N2,2 (0.5)和N3,2 (0.5)，不必计算，因为 计算它们需要的i>2时的Ni,1 (0.5)=0， 所以知N2,2 (0.5)=N3,2 (0.5)=0。这样代 入公式计算P(0.5)，有： ) 1 P 0 0.5 ( P 3 (0.5) P 3,2 N 2 (0.5) P 2,2 N 1 (0.5) P 1,2 N 0 (0.5) P 0,2 P(0.5) N =  + +  +  =  + 

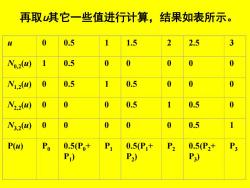
再取其它一些值进行计算，结果如表所示。 0.5 1.5 2 2.5 3 N0.2(0 0.5 0 0 0 0 N1.2(W) 0.5 0.5 N2.20 0.5 1 0.5 N3.20 0.5 P(u) Po 0.5Po+ P 0.5P1+ P2 0.5P2+ P3 P) P2) P3)

再取u其它一些值进行计算，结果如表所示。 u 0 0.5 1 1.5 2 2.5 3 N0,2 (u) 1 0.5 0 0 0 0 0 N1,2 (u) 0 0.5 1 0.5 0 0 0 N2,2 (u) 0 0 0 0.5 1 0.5 0 N3,2 (u) 0 0 0 0 0 0.5 1 P(u) P0 0.5(P0+ P1 ) P1 0.5(P1+ P2 ) P2 0.5(P2+ P3 ) P3

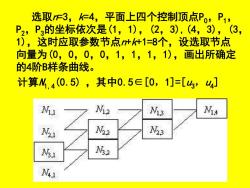
选取F3,仁4，平面上四个控制顶点Po,P1, P2,P3的坐标依次是(1,1)，(2,3)，(4,3)，(3， 1)，这时应取参数节点什k件1=8个，设选取节点 向量为(0,0,0,0,1,1,1,1)，画出所确定 的4阶B样条曲线。 计算M.4(0.5),其中0.5∈[0,1]=[，w4] 12 N13 A 2 3 1 2

选取n=3，k=4，平面上四个控制顶点P0，P1， P2，P3的坐标依次是(1，1)，(2，3),(4，3)，(3， 1)，这时应取参数节点n+k+1=8个，设选取节点 向量为(0，0，0，0，1，1，1，1)，画出所确定 的4阶B样条曲线。 计算N1,4(0.5) ，其中0.5∈[0，1]=[u3，u4 ]

N1(0.5)=1,而对i+3,W,1(0.5)=0 2,20.5-050x0+1-051=0.5 0-0 1-0 g,20.50501+1-0.50-0.5 ×l+ 1-0 -0 N1,3(0.50.5-0 1-0.5 0+ ×0.5=0.25 1-0 1-0 N2,3(0.5)0.5-0 -0.5 ×0.5+ ×0.5=0.5 1-0 1-0 N,40.5)-9 .5-0 ×0.25+ 1-0.5 ×0.5=0.375 1-0 1-0

N 3,1(0.5)=1，而对i≠3，Ni,1(0.5)=0。 0.5 0.375 1 0 1 0.5 0.25 1 0 0.5 0 (0.5) 1,4 N 0.5 0.5 1 0 1 0.5 0.5 1 0 0.5 0 (0.5) 2,3 N 0.5 0.25 1 0 1 0.5 0 1 0 0.5 0 (0.5) 1,3 N 0 0.5 1 0 1 0.5 1 1 0 0.5 0 (0.5) 3,2 N 1 0.5 1 0 1 0.5 0 0 0 0.5 0 (0.5) 2,2 N  = − −  + − − =  = − −  + − − =  = − −  + − − =  = − −  + − − =  = − −  + − − =

用类似的过程可计算求出： N0,40.5)=0.125 N2,40.50.375 N3,40.5)=0.125 曲线上对应参数0.5的点是： P(0.5)=N0,40.5》Po+N1,40.5》P +N2,40.5》2+N3,40.5P3 =(2.75,2.5)

用类似的过程可计算求出： (0.5) 0.125 3,4 N (0.5) 0.375 2,4 N (0.5) 0.125 0,4 N = = = 曲线上对应参数u=0.5的点是： (2.75,2.5) 3 (0.5) P 3,4 N 2 (0.5) P 2,4 N 1 (0.5) P 1,4 N 0 (0.5) P 0,4 P(0.5) N = +  +  =  + 