南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第21章 基本概念

基本概念 离散数学一图论初步 南京大学计算机科学与技术系
基本概念 离散数学─图论初步 南京大学计算机科学与技术系

急售扇 内容提要 ING 。图的定义 ·用图建模 ·图的表示 ·图的运算 ·图的同构 2
内容提要 图的定义 用图建模 图的表示 图的运算 图的同构 2
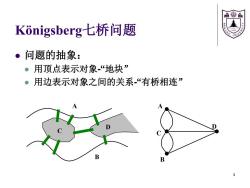
&感 Konigsberg七桥问题 ·问题的抽象: 。用顶点表示对象“地块” 。用边表示对象之间的关系“有桥相连
Königsberg七桥问题 问题的抽象: 用顶点表示对象-“地块” 用边表示对象之间的关系-“有桥相连” C D A B A C B D 3
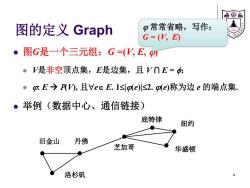
雪扇 图的定义Graph p常常省略,写作: G=(V,E) o 图G是一个三元组:G=(V,E, 。V是非空顶点集,E是边集,且V∩E=: ●mE→r,且e∈E.1≤l(e)s2.o(e)称为边e的端点集 。举例(数据中心、通信链接) 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶
图的定义 Graph 图G是一个三元组:G =(V, E, ) V是非空顶点集,E是边集,且 V ⋂ E = ; : E (V), 且e E. 1|(e)|2. (e)称为边 e 的端点集. 举例(数据中心、通信链接) 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 常常省略,写作: G = (V, E) 4

&食嘉 图的定义(续) ·图G=(V,E,p)是简单图,如果 。每条边有2个端点,即:e∈E.lp(e川=2,并且 。不同边有不同端点集,即:如果e1≠e2,则p(ei)≠p(e2) ·图G=(V,E,φ)是伪图,如果 。存在一条只有1个端点的边,即:3eo∈E.p(eo=1,或者 。有两条边具有相同的端点集,即:3e≠e2p(e)=p(e2)
图的定义(续) 图G = (V, E, )是简单图,如果 每条边有2个端点,即: e E. |(e)| = 2,并且 不同边有不同端点集,即:如果e1 e2 ,则(e1 ) (e2 ) 图G = (V, E, )是伪图,如果 存在一条只有1个端点的边,即: e0E.|(e0 )| = 1,或者 有两条边具有相同的端点集,即: e1 e2 .(e1 )=(e2 ) 5
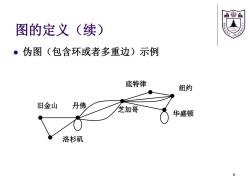
般线扇 图的定义(续) NG ·伪图(包含环或者多重边)示例 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶 6
图的定义(续) 伪图(包含环或者多重边)示例 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 6
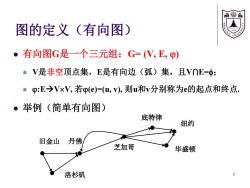
&感 2 图的定义(有向图) ·有向图G是一个三元组:G=(V,E,φ) 。V是非空顶点集,E是有向边(弧)集,且V∩E=中: ●p:E→VxV,若p(e)=(u,v),则u和v分别称为e的起点和终点. ·举例(简单有向图) 底特律 纽约 旧金山丹佛 芝加哥 华盛顿 洛杉矶
图的定义(有向图) 有向图G是一个三元组:G= (V, E, ) V是非空顶点集,E是有向边(弧)集,且V⋂E=; :EVV, 若(e)=(u, v), 则u和v分别称为e的起点和终点. 举例(简单有向图) 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 7
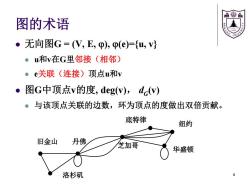
急售鼎 图的术语 ·无向图G=(V,E,p),p(e)={u,} 。u和v在G里邻接(相邻) ●e关联(连接)顶点u和v 。图G中顶点v的度,deg(v),dcv) 。与该顶点关联的边数,环为顶点的度做出双倍贡献。 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶 8
图的术语 无向图G = (V, E, ), (e)={u, v} u和v在G里邻接(相邻) e关联(连接)顶点u和v 图G中顶点v的度, deg(v), dG (v) 与该顶点关联的边数,环为顶点的度做出双倍贡献。 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 8

&售嘉 握手定理 。无向图G有m条边,n个顶点v1,vm ∑dy,)=2m i=1 ·推论:无向图中奇数度顶点必是偶数个。 9
握手定理 无向图G有m条边,n个顶点v1 , …vn . 推论:无向图中奇数度顶点必是偶数个。 d v m n i i ( ) 2 1 9

款感 图的术语(续) U ·有向图G=(V,E,p),p()=(u,v) ●u是e的起点,v是e的终点 。假设u≠v,u邻接到v,v从u邻接 ·有向图中顶点的出度和入度 。dc+v)=以v为始点的边的条数,degt(w) 。de(w)=以v为终点的边的条数,deg(w) ·有向图中各顶点的出度之和等于入度之和。 ∑vev deg"((W)=∑vev deg(v)=E ●有向图的底图 10
图的术语(续) 有向图G =(V, E, ), (e)=(u, v) u是e的起点,v是e的终点 假设 uv,u邻接到v,v从u邻接 有向图中顶点的出度和入度 dG + (v) = 以v为始点的边的条数, deg+ (v) dG - (v) = 以v为终点的边的条数, deg- (v) 有向图中各顶点的出度之和等于入度之和。 vV deg+ (v) = vV deg- (v) =|E| 有向图的底图 10
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)关系——第14章 偏序关系.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)代数系统——第20章 布尔代数.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)代数系统——第19章 代数格.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)代数系统——第18章 循环群与群同构.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)代数系统——第17章 子群与拉格朗日定理.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)代数系统——第16章 群论导引.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)关系——第13章 关系的闭包、等价关系.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)代数系统——第15章 代数系统.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)计数与离散概率——第11章 离散概率.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)集合论——第8章 数论初步.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)关系——第12章 关系及其运算.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)集合论——第9章 归纳与递归.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)计数与离散概率——第10章 基本计数技术.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)集合论——第7章 集合的基数.pdf
- 西安电子科技大学:《线性代数》课程教学资源(课件讲义)线性代数讲义(第4-8章).pdf
- 西安电子科技大学:《线性代数》课程教学资源(课件讲义)线性代数讲义(第1-3章).pdf
- 西安电子科技大学:《线性代数》课程教学资源(教学大纲)Linear Algebra(主讲:李仁先).docx
- 南京大学:《计算方法 Numerical method》课程教学资源(课件讲稿)计算方法16.pdf
- 南京大学:《计算方法 Numerical method》课程教学资源(课件讲稿)计算方法15.pdf
- 南京大学:《计算方法 Numerical method》课程教学资源(课件讲稿)计算方法14.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第22章 图的连通性.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第23章 欧拉图、哈密尔顿图.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第24章 最短通路问题.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第25章 二部图与匹配.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第26章 树的基本概念.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第27章 树的应用.pdf
- 南京大学:《离散数学 Discrete Mathmatics》课程教学资源(课件讲稿,2018)图论——第28章 生成树(任课教师:史颖欢).pdf
- 《离散数学及其应用》参考书籍(英文原版,第七版,作者:Kenneth H. Rosen,2012)Discrete Mathematics and Its Applications(SEVENTH EDITION).pdf
- 山西师范大学:《高等数学B》课程教学大纲.docx
- 武昌首义学院:《高等数学》课程教学大纲(OBE模式)高等数学A1 Advanced Mathematics A1(打印版).pdf
- 武昌首义学院:《高等数学》课程教学大纲(OBE模式)高等数学A2 Advanced Mathematics A2.pdf
- 武昌首义学院:《高等数学》课程教学大纲(OBE模式)高等数学B1 Advanced Mathematics B1.pdf
- 武昌首义学院:《工程数学》课程教学大纲(非OBE模式)工程数学 Engineering Mathematics.pdf
- 武昌首义学院:《高等数学》课程教学大纲(OBE模式)高等数学B2 Advanced Mathematics B2.pdf
- 武昌首义学院:《微积分》课程教学大纲(OBE模式)微积分A1 Calculus A1.pdf
- 武昌首义学院:《微积分》课程教学大纲(OBE模式)微积分A2 Calculus A2.pdf
- 武昌首义学院:《微积分》课程教学大纲(OBE模式)微积分B1 Calculus B1.pdf
- 武昌首义学院:《微积分》课程教学大纲(OBE模式)微积分B2 Calculus B2.pdf
- 武昌首义学院:《线性代数》课程教学大纲(OBE模式)线性代数 Linear Algebra.pdf
- 武昌首义学院:《复变函数与积分变换》课程教学大纲(OBE模式)复变函数与积分变换 Complex Function and Integral Transform.pdf
