《数据结构》课程教学资源（作业习题）练习题及答案6

1.设一棵完全二叉树有700个结点，圆共有350个叶子结点。 答：最快方法：用叶子数=21=35 2.设一棵完全二又树具有1000个结点，则此完全二又树有500个叶子结点，有499个度为2的结点， 有1个结点只有非空左子树，有0个结点只有非空右子树。 答：最快方法：用叶子数=121=500，m2m-1=499。另外，最后一结点为2i属于左叶子，右叶子是空 的，所以有1个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况，所以非空右子树数=0， 一操含有个结点的k叉树，可能达到的最大深度为 最小深度为2 答：当k1(单叉树)时应该最深，深度=n(层)当k=n-1(m1叉树)时应该最浅，深度=2（层），但不 包括=0或1时的特例情况。教材答案是“完全k叉树”，未定量。) 4.用5个权值3,2,4,5,1}构造的哈夫曼(Huffman)树的带权路径长度是33 解：先构造哈夫曼树，得到各叶子的略径长度之后便可求出WPL=(4+5+3)×2+（1十2)×3=33 15) (注：两个合并值先后不同会导致编码不同，即哈夫曼编码不唯一) 5 3 (注：合并值应排在叶子值之后) (注：原题为选择题：A.32 B33 C.34 D.15) (C)1.不含任何结点的空树 （A）是一棵树 (B)是一棵二叉树： (C)是一棵树也是一棵二叉树： (D)既不是树也不是二叉树 答：以前的标答是B,因为那时树的定义是n≥1 (C)2。二叉树是非线性数据结构，所以 (A)它不能用顺序存储结构存储 (B)它不能用链式存储结构存储 (C)顺序存储结构和链式存储结构都能存储(D)顺序存储结构和链式存储结构都不能使用 (C)3.只有(>0)个结点的完全二叉树的深度为 (A)Tlog:(n)7 (B)Llogz(n)J (C)Llog=(n)+1 (D)Tlogz(n)+17 注1：「x表示不小于x的最小整数：Lx表示不大于x的最大整数，它们与]含义不同： 注2：选(A)是错误的。例如当n为2的整数幂时就会少算一层。似孔log2()+1是对的 (A)4.把一棵树转换为二叉树后，这棵二叉树的形态是 (A)唯一的 (B)有多种 (C)有多种，但根结点都没有左孩子 （D)有多种，但根结点都没有右孩子 5.【94程PI1】从供选择的答案中，选出应填入下面叙述？内的最确切的解答，把相应编号写在 答卷的对应栏内。 树是结点的有限集合，它A根结点，记为T。其余的结点分成为m(m≥0)个B 的集合T1,T2,.,Tm,每个集合又都是树，此时结点T称为T:的父结点，T称为T的子结点(1≤i ≤m)。 个结点的子结点个数为该结点的C 供选择的答案 A:①有0个或1个 ②有0个或多个 ③有且只有1个 ④有1个或1个以上 B: ①互不相交 ②允许相交 ③允许叶结点相交 ④允许树枝结点相交 C:①权 ②维数 ③次数（或度） ④序 答案：ABC=1,1,3

1 1.设一棵完全二叉树有 700 个结点，则共有 350 个叶子结点。 答：最快方法：用叶子数＝[n/2]＝350 2.设一棵完全二叉树具有 1000 个结点，则此完全二叉树有 500 个叶子结点，有 499 个度为 2 的结点， 有 1 个结点只有非空左子树，有 0 个结点只有非空右子树。 答：最快方法：用叶子数＝[n/2]＝500 ，n2=n0-1=499。 另外，最后一结点为 2i 属于左叶子，右叶子是空 的，所以有 1 个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况，所以非空右子树数＝0. 3. 一棵含有 n 个结点的 k 叉树，可能达到的最大深度为 n ，最小深度为 2 。 答：当 k=1(单叉树)时应该最深，深度＝n（层）；当 k=n-1（n-1 叉树）时应该最浅，深度＝2（层），但不 包括 n=0 或 1 时的特例情况。教材答案是“完全 k 叉树”，未定量。) 4. 用 5 个权值{3, 2, 4, 5, 1}构造的哈夫曼（Huffman）树的带权路径长度是 33 。 解：先构造哈夫曼树，得到各叶子的路径长度之后便可求出 WPL＝（4＋5＋3）×2＋（1＋2）×3=33 (15) (9) (6) （注：两个合并值先后不同会导致编码不同，即哈夫曼编码不唯一） 4 5 3 (3) （注：合并值应排在叶子值之后） 1 2 （注：原题为选择题：Ａ．32 Ｂ．33 Ｃ．34 Ｄ．15） （ C ）1． 不含任何结点的空树 。 （Ａ）是一棵树; （Ｂ）是一棵二叉树; （Ｃ）是一棵树也是一棵二叉树; （Ｄ）既不是树也不是二叉树 答：以前的标答是 B，因为那时树的定义是 n≥1 （ C ）2．二叉树是非线性数据结构，所以 。 （Ａ）它不能用顺序存储结构存储; （Ｂ）它不能用链式存储结构存储; （Ｃ）顺序存储结构和链式存储结构都能存储; （Ｄ）顺序存储结构和链式存储结构都不能使用 （ C ）3. 具有 n(n>0)个结点的完全二叉树的深度为 。 (Ａ) log2(n) (Ｂ) log2(n) (Ｃ) log2(n) +1 (Ｄ) log2(n)+1 注 1：x 表示不小于 x 的最小整数； x表示不大于 x 的最大整数，它们与[ ]含义不同！ 注 2：选（A）是错误的。例如当 n 为 2 的整数幂时就会少算一层。似乎log2(n) +1是对的？ （ A ）4．把一棵树转换为二叉树后，这棵二叉树的形态是 。 （Ａ）唯一的 （Ｂ）有多种 （Ｃ）有多种，但根结点都没有左孩子 （Ｄ）有多种，但根结点都没有右孩子 5. 【94 程 P11】 从供选择的答案中，选出应填入下面叙述 ？ 内的最确切的解答，把相应编号写在 答卷的对应栏内。 树是结点的有限集合，它 A 根结点，记为 T。其余的结点分成为 m（m≥0）个 B 的集合 T1，T2，.，Tm，每个集合又都是树，此时结点 T 称为 Ti 的父结点，Ti称为 T 的子结点（1≤i ≤m）。一个结点的子结点个数为该结点的 C 。 供选择的答案 A： ①有 0 个或 1 个 ②有 0 个或多个 ③有且只有 1 个 ④有 1 个或 1 个以上 B: ①互不相交 ② 允许相交 ③ 允许叶结点相交 ④ 允许树枝结点相交 C： ①权 ② 维数 ③ 次数（或度） ④ 序 答案：ABC＝1，1，3

6.【5程P13】从供选择的答案中，选出应填入下面叙述？内的最确切的解答，把相应编号写在 答卷的对应栏内。 二叉树A 。在完全的二叉树中，若一个结点没有B,则它必定是叶结点。每棵树都能惟一地转 换成与它对应的二叉树。由树转换成的二叉树里，一个结点N的左子女是N在原树里对应结点的C 而N的右子女是它在原树里对应结点的D。 供选择的答案 A:①是特殊的树②不是树的特殊形式③是两棵树的总称④有是只有二个根结点的树形结构 B:①左子结点②右子结点③左子结点或者没有右子结点 ④兄弟 C~D:①最左子结点 ②最右子结点 ③最邻近的右兄弟 ④最邻近的左兄弟 ⑤最左的兄弟 ⑧最右的兄弟 答案：A= B C= D= 答案：ABCDE=2,1,1,3 2.《01年计算机研题】设如下图所示的二叉树B的存储结构为二叉链表，【Oot为根指针，结点结构为： (Ichild,.data,rchild)。其中Ichild,rehild分别为指向左右孩子的指针， C的结点类型定义如下： data为字符型，root为根指针，试回答下列问要： 对下列二叉树B,执行下列算法traversal(roo,试指出其输出结 struct node char data; 2.假定二叉树B共有n个结点，试分析算法traversal(roo)的时间复 struct node 'lchild.rchild: 朵度。（共8分） C算法如下 void traversal(struct node*root) 二叉树B G f(root) printfr%c"root->data) 解：这是“先根再左再根再右”，比前序遍历多打印各结点一次，输 traversal(root->Ichild): 出结果为：ABCCEEBADFFDGG 特点：①每个结点肯定都会被打印两次 ②但出现的顺序不同，其 traversal(root-rchild) 规律是：凡是有左子树的结点，必间隔左子树的全部结点后再重复 出现：如A,B,D等结点。反之马上就会重复出现。如C,E,F, G等结点。 时间复杂度以访间结点的次数为主，精确值为2*，时间渐近度为O() 3.【01年计算机研题】【严题集6.27③】给定二叉树的两种遍历序列， 分别是 前序遍历序列 D,A,C, E,B,H,F,G,1: 试画出二又树B, 中序遍历序列：D.CBE,H,AG,E, 并简述由任意二叉树B的前序遍历序列和中序遍历序列求二叉树B的思想方法。 解：方法是：由前序先确定r0ot,由中序可确定00t的左、右子树。然后由其左子树的元素集合和右子树 的集合对应前序速历序列中的元素集合，可继续确定r0t的左右孩子。将他们分别作为新的root,不断递 归，则所有元素都将被唯一确定，问题得解

2 6. 【95 程 P13】 从供选择的答案中，选出应填入下面叙述 ？ 内的最确切的解答，把相应编号写在 答卷的对应栏内。 二叉树 A 。在完全的二叉树中，若一个结点没有 B ，则它必定是叶结点。每棵树都能惟一地转 换成与它对应的二叉树。由树转换成的二叉树里，一个结点 N 的左子女是 N 在原树里对应结点的 C ， 而 N 的右子女是它在原树里对应结点的 D 。 供选择的答案 A： ①是特殊的树 ②不是树的特殊形式 ③是两棵树的总称 ④有是只有二个根结点的树形结构 B: ①左子结点 ② 右子结点 ③ 左子结点或者没有右子结点 ④ 兄弟 C～D： ①最左子结点 ② 最右子结点 ③ 最邻近的右兄弟 ④ 最邻近的左兄弟 ⑤ 最左的兄弟 ⑥ 最右的兄弟 答案：A= B= C= D＝ 答案：ABCDE＝2，1，1，3 2.〖01 年计算机研题〗设如下图所示的二叉树 B 的存储结构为二叉链表，root 为根指针，结点结构为： （lchild,data,rchild）。其中 lchild，rchild 分别为指向左右孩子的指针， data 为字符型，root 为根指针，试回答下列问题： 1. 对下列二叉树 B，执行下列算法 traversal(root)，试指出其输出结 果； 2. 假定二叉树 B 共有 n 个结点，试分析算法 traversal(root)的时间复 杂度。（共 8 分） 二叉树 B 解：这是“先根再左再根再右”，比前序遍历多打印各结点一次，输 出结果为：A B C C E E B A D F F D G G 特点：①每个结点肯定都会被打印两次；②但出现的顺序不同，其 规律是：凡是有左子树的结点，必间隔左子树的全部结点后再重复 出现；如 A，B，D 等结点。反之马上就会重复出现。如 C，E，F， G 等结点。 时间复杂度以访问结点的次数为主，精确值为 2*n，时间渐近度为 O(n). 3. 〖01 年计算机研题〗【严题集 6.27③】给定二叉树的两种遍历序列，分别是： 前序遍历序列：D，A，C，E，B，H，F，G，I； 中序遍历序列：D，C，B，E，H，A，G，I，F， 试画出二叉树 B，并简述由任意二叉树 B 的前序遍历序列和中序遍历序列求二叉树 B 的思想方法。 解：方法是：由前序先确定 root，由中序可确定 root 的左、右子树。然后由其左子树的元素集合和右子树 的集合对应前序遍历序列中的元素集合，可继续确定 root 的左右孩子。将他们分别作为新的 root，不断递 归，则所有元素都将被唯一确定，问题得解。 D A C F E G B H I A B D C F G E C 的结点类型定义如下： struct node {char data; struct node *lchild, rchild; }; C 算法如下： void traversal(struct node *root) {if (root) {printf(“%c”, root->data); traversal(root->lchild); printf(“%c”, root->data); traversal(root->rchild); } }

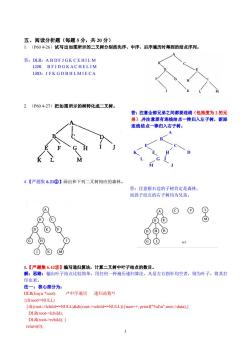
五、阅读分析题（每题5分，共20分） 1(P604-26)试写出如图所示的二又树分别按先序、中序、后序遍历时得到的结点序列， 答：DLR:ABDFJGKCEHILM LDR:BFJDGKACHELIM LRD:JFKGDBHLMIECA 2.(P604-27)把如图所示的树转化成二叉树。 答：注意全部兄弟之间都要连线（包括度为2的兄 弟)并注意原有连线结点一律归入左子树，新 连线结点一律归入右子树。 A M 4.【严题集6.21②】画出和下列二叉树相应的森林 答：注意根右边的子树肯定是森林， 而孩子结点的右子树均为兄弟。 ®包 ⊙①⑧ ⊙▣ ⊙① e 1.【严题集6.42③】编写递归算法，计算二叉树中叶子结点的数目。 解：思路：输出叶子结点比较简单，用任何一种遍历递归算法，凡是左右指针均空者，则为叶子，将其打 印出来。 法一：核心部分为 DLR(liuyu*root) 中序遍历 递归函数 fif(rootl=NULL) (if((root->Ichild==NULL)&&(root->rchild==NULL))sum++;printf("%d\n",root->data).) DLR(root->lchild). DLR(root->rchild): return(); 3

3 五、阅读分析题（每题 5 分，共 20 分） 1. （P60 4-26）试写出如图所示的二叉树分别按先序、中序、后序遍历时得到的结点序列。 答：DLR：A B D F J G K C E H I L M LDR: B F J D G K A C H E L I M LRD：J F K G D B H L M I E C A 2. （P60 4-27）把如图所示的树转化成二叉树。 答：注意全部兄弟之间都要连线（包括度为 2 的兄 弟）,并注意原有连线结点一律归入左子树，新添 连线结点一律归入右子树。 A B E C K F H D L G I M J 4.【严题集 6.21②】画出和下列二叉树相应的森林。 答：注意根右边的子树肯定是森林， 而孩子结点的右子树均为兄弟。 1.【严题集 6.42③】编写递归算法，计算二叉树中叶子结点的数目。 解：思路：输出叶子结点比较简单，用任何一种遍历递归算法，凡是左右指针均空者，则为叶子，将其打 印出来。 法一：核心部分为： DLR(liuyu *root) /*中序遍历 递归函数*/ {if(root!=NULL) {if((root->lchild==NULL)&&(root->rchild==NULL)){sum++; printf("%d\n",root->data);} DLR(root->lchild); DLR(root->rchild); } return(0);

6.【严题集626③】假设用于通信的电文仅由8个字母组成，字母在电文中出现的频率分别为0.07,0.19， 0.02,0.06,0.32,0.03,0.21,0.10。试为这8个字母设计哈夫曼编码。解：方案1：哈夫曼编码 先将概率放大10倍，以方便构造哈夫曼树。 w=7,19,2,6.32,3.21,10,按哈夫曼规则：【(2,3)，61，(7,10】，.19,21,32 (100) 0入1 (40) 19 21 3立(28) S171(1) 213 06(5) 23 字母编号对应编码出现频率 1100 006 10 0.32 1 1101 010 WPL=2(0.19+0.32+0.21+4(0.07+0.06+0.10+5(0.02+0.03=1.44+0.92+0.25=2.61 4

4 } 6. 【严题集 6.26③】假设用于通信的电文仅由 8 个字母组成，字母在电文中出现的频率分别为 0.07，0.19， 0.02，0.06，0.32，0.03，0.21，0.10。试为这 8 个字母设计哈夫曼编码。解：方案 1；哈夫曼编码 先将概率放大 100 倍，以方便构造哈夫曼树。 w={7,19,2,6,32,3,21,10}，按哈夫曼规则：【[（2,3），6], (7,10)】, .19, 21, 32 （100） （40） （60） 19 21 32 （28） （17） （11） 7 10 6 （5） 2 3 WPL＝2(0.19+0.32+0.21)+4(0.07+0.06+0.10)+5(0.02+0.03)=1.44+0.92+0.25=2.61 0 1 0 1 0 1 19 21 32 0 1 0 1 0 1 7 10 6 0 1 2 3 字母编号 对应编码 出现频率 1 1100 0.07 2 00 0.19 3 11110 0.02 4 1110 0.06 5 10 0.32 6 11111 0.03 7 01 0.21 8 1101 0.10