福州大学:《化工原理》课程教学课件(PPT讲稿)第四章 颗粒的沉降

5.颗粒的沉降 5.1概述 5.2颗粒的沉降运动 5.3沉降分离设备
5.颗粒的沉降 5.1 概述 5.2颗粒的沉降运动 5.3沉降分离设备

5.1概述 本章考察流固两相物系中固体颗粒与流体间的 相对运动。在流固两相物系中,不论作为连续相的 流体处于静止还是作莫种运动,只要固体颗粒的密 度P大于流体的密度P,那么在重力场中,固体颗 粒将在重力方向上与流体做相对运动,在离心力场 中,测与流体作离心力方向上的相对运动
5.1 概述 本章考察流固两相物系中固体颗粒与流体间的 相对运动。在流固两相物系中,不论作为连续相的 流体处于静止还是作莫种运动,只要固体颗粒的密 度 大于流体的密度 ,那么在重力场中,固体颗 粒将在重力方向上与流体做相对运动,在离心力场 中,则与流体作离心力方向上的相对运动

5.2颗粒的沉降运动 5.2.1流体对固体颗粒的绕流 5.2.2静止流体中颗粒的自由沉降
5.2 颗粒的沉降运动 5.2.1 流体对固体颗粒的绕流 5.2.2 静止流体中颗粒的自由沉降

5.2.1流体对固体颗粒的绕流 流体与固体颗粒之间的相对运动可分为以下三 种情况: ①颗粒静止,流体对其做绕流; ②流体静止,颗粒作沉降运动: ③颗粒与流体都运动,但保持一定的相对运动
流体与固体颗粒之间的相对运动可分为以下三 种情况: ①颗粒静止,流体对其做绕流; ②流体静止,颗粒作沉降运动; ③颗粒与流体都运动,但保持一定的相对运动。 5.2.1 流体对固体颗粒的绕流

(1)两种曳力一表面曳力和形体曳力 回顾第1章流体沿固体壁面流过的阻力分为两类:表 皮阻力(即表面摩擦阻力)和形体阻力(边界层分离产 生旋涡),绕流时颗粒受到流体的总曳力: F。=表面曳力+形体曳力
(1)两种曳力—表面曳力和形体曳力 回顾第1章流体沿固体壁面流过的阻力分为两类:表 皮阻力(即表面摩擦阻力)和形体阻力(边界层分离产 生旋涡),绕流时颗粒受到流体的总曳力:

(1)两种曳力一表面曳力和形体曳力 F,与流体P、4、相对流速u有关,而且受颗粒的 形状与定向的影响,问题较为复杂。至今,只有几何 形状简单的少数情况才可以得到F。的理论计算式。例 如,粘性流体对球体的低速绕流(也称爬流)时F,的 理论式即斯托克律(Stokes)定律为: F)=3πd,u 当流速较高时,Stokes定律不成立。因此,对一 般流动条件下的球形颗粒及其其他形状的颗粒,F,的 数值尚需通过实验解决
(1)两种曳力—表面曳力和形体曳力 FD与流体 、 、相对流速 有关,而且受颗粒的 形状与定向的影响,问题较为复杂。至今,只有几何 形状简单的少数情况才可以得到FD的理论计算式。例 如,粘性流体对球体的低速绕流(也称爬流)时FD的 理论式即斯托克律(Stokes)定律为: 当流速较高时,Stokes定律不成立。因此,对一 般流动条件下的球形颗粒及其其他形状的颗粒,FD的 数值尚需通过实验解决。 u FD = 3 dp u
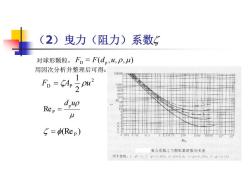
(2)曳力(阻力)系数5 对球形颗粒,F。=F(d,u,P,) 用因次分析并整理后可得: 。=42m dup Rep = 从 =(Rep) R 曳力系数:与期拉宙诸数的关系 房中准线,1-11¥4=公00:3=0,6,4一V-0,20,行一◆-05
(2)曳力(阻力)系数 对球形颗粒, 用因次分析并整理后可得: = ( , , , ) FD F dp u (Re ) = P dp u Re P = 2 D P 2 1 F = A u

(2)曳力(阻力)系数5 球形颗粒(w=1)的曲线在不同的雷诺数范围内可用公式表示如下: 24 Rep<2,层流区,Sokes定律区:5= Rep 2<Rep<500,过渡区,A1len定律区: 18.5 5= Repo6 500<Rep<2×l05,湍流区,Newton定律区: 5≈0.44
球形颗粒 ( = 1) 的曲线在不同的雷诺数范围内可用公式表示如下: Re P 2 ,层流区,Sokes定律区: Re P 24 = 2 Re P 500 ,过渡区,Allen定律区: 0.6 Re P 18.5 = ,湍流区,Newton定律区: 5 500 Re P 210 0.44 (2)曳力(阻力)系数

5.2.2静止流体中颗粒的自由沉降 (1)沉降的加速段 将一个表面光滑的球形颗粒置于静止的流体中,若,颗粒在重力 的作用下沿重力方向作沉降运动,此时颗粒受到哪些力的作用呢? Fa Fg=mg= dy pv8 6 =d,pg 6 3o3 1
5.2.2 静止流体中颗粒的自由沉降 (1)沉降的加速段 将一个表面光滑的球形颗粒置于静止的流体中,若,颗粒在重力 的作用下沿重力方向作沉降运动,此时颗粒受到哪些力的作用呢? Fg mg d P g 3 P 6 = = Fb dP g 3 6 = 2 2 2 2 1 2 4 1 FD AP u d P u = =

5.2.2静止流体中颗粒的自由沉降 根据牛顿第二定律得: ∑F=Fg-F。-F。=ma= 4 4,p,8-4,pg- 22交 du 6 6 6 dr 或者: 35 dr p2 Pp du 开始瞬间,u=0,dz最大,颗粒作加速运动
根据牛顿第二定律得: d du F Fg Fb FD m a d P P g d P g d P u d P P 3 3 2 2 3 2 6 1 6 6 4 = − − = = − − = 或者 : 2 4 3 ( ) u d g d du P P P P − − = 开始瞬间, u = 0 , d 最大,颗粒作加速运动。 du 5.2.2 静止流体中颗粒的自由沉降
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第三章 流体通过颗粒层的流动.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第二章 流体输送机械.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第一章 流体流动.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)绪论.ppt
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第七章 蒸馏和吸收塔设备.ppt
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第六章 吸热(吸收).ppt
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第四章 传热.ppt
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第三章 机械分离.ppt
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第二章 流体输送机械.ppt
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第一章 流体流动FLUID FLOW MOMENTUM TRANSFER(FLUID MECHANICS).ppt
- 曲阜师范大学:《煤化工工艺学》课程教学大纲.pdf
- 曲阜师范大学:《化学工艺学》课程教学大纲.pdf
- 曲阜师范大学:《化工制图》课程教学大纲.pdf
- 曲阜师范大学:《化工原理》课程教学大纲.pdf
- 曲阜师范大学:《化工仪表及自动化》课程教学大纲.pdf
- 曲阜师范大学:《化工设计》课程教学大纲.pdf
- 曲阜师范大学:《化工基础》课程教学大纲.pdf
- 曲阜师范大学:《化工安全工程学》课程教学大纲.pdf
- 曲阜师范大学:《计算机化工应用》课程教学大纲.pdf
- 曲阜师范大学:《化学反应工程》课程教学大纲.pdf
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第六章 气体吸收.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第七章 液体精馏.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第八章 气液传质设备.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第九章 液液萃取.ppt
- 福州大学:《化工原理》课程教学课件(PPT讲稿)第十章 固体干燥.ppt
- 南京林业大学:《化工原理》课程教学资源(PPT课件)绪论.ppt
- 南京林业大学:《化工原理》课程教学资源(PPT课件)第一章 流体流动.ppt
- 南京林业大学:《化工原理》课程教学资源(PPT课件)第五章 蒸发.ppt
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验一 流体流动阻力测定实验.doc
- 南京林业大学:《化工原理》课程教学资源(PPT课件)第一章 蒸馏.ppt
- 南京林业大学:《化工原理》课程教学资源(PPT课件)第二章 吸收.ppt
- 南京林业大学:《化工原理》课程教学资源(PPT课件)第三章 蒸馏和吸收塔设备.ppt
- 南京林业大学:《化工原理》课程教学资源(PPT课件)第四章 干燥.ppt
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验二 离心泵特性曲线测定实验.doc
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验三 恒压过滤常数测定实验.doc
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验四 传热系数测定实验.doc
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验五 精馏实验.doc
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验六 吸收实验.doc
- 南京林业大学:《化工原理》课程教学资源(实验指导)实验七 干燥实验.doc
- 广东工业大学:《化工原理》课程电子教案(PPT教学课件)第五章 蒸馏.ppt
