西安电子科技大学：《算法设计技术 Algorithms Design Techniques》课程教学资源（PPT课件讲稿）Coping with Hardness（Chapter 13 Backtracking Chapter 14 Randomized Algorithms Chapter 15 Approximation Algorithms）

Coping with Hardness Backtracking:suitable for those problems that exhibit good average time complexity.This methodology is based on a methodic examination of the implicit state space induced by the problem instance under study.In the process of exploring the state space of the instance,some pruning takes place. Randomized Algorithms:Based on the probabilistic notion of accuracy. a Approximation Algorithms:Compromise on the quality of solution in return for faster solutions

Coping with Hardness ◼ Backtracking: suitable for those problems that exhibit good average time complexity. This methodology is based on a methodic examination of the implicit state space induced by the problem instance under study. In the process of exploring the state space of the instance, some pruning takes place. ◼ Randomized Algorithms: Based on the probabilistic notion of accuracy. ◼ Approximation Algorithms: Compromise on the quality of solution in return for faster solutions

Backtracking In many real world problems,a solution can be obtained by exhaustively searching through a large but finite number of possibilities.Hence,the need arose for developing systematic techniques of searching,with the hope of cutting down the search space to possibly a much smaller space. Here,we present a general technique for organizing the search known as backtracking.This algorithm design technique can be described as an organized exhaustive search which often avoids searching all possibilities

Backtracking ◼ In many real world problems, a solution can be obtained by exhaustively searching through a large but finite number of possibilities. Hence, the need arose for developing systematic techniques of searching, with the hope of cutting down the search space to possibly a much smaller space. ◼ Here, we present a general technique for organizing the search known as backtracking. This algorithm design technique can be described as an organized exhaustive search which often avoids searching all possibilities

The 3-Coloring Problem Given an undirected graph G=(,E),it is required to color each vertex in Vwith one of three colors,say 1, 2,and 3,such that no two adjacent vertices have the same color.We call such a coloring legal;otherwise, if two adjacent vertices have the same color,it is illegal. A coloring can be represented by an n-tuple(G, G2,,Cn)such that c∈{1,2,3}，1≤kn. For example,(1,2,2,3,1)denotes a coloring of a graph with five vertices

The 3-Coloring Problem ◼ Given an undirected graph G=(V, E), it is required to color each vertex in V with one of three colors, say 1, 2, and 3, such that no two adjacent vertices have the same color. We call such a coloring legal; otherwise, if two adjacent vertices have the same color, it is illegal. ◼ A coloring can be represented by an n-tuple (c1 , c2 , …, cn ) such that ci{1, 2, 3}, 1in. ◼ For example, (1, 2, 2, 3, 1) denotes a coloring of a graph with five vertices

The 3-Coloring Problem There are 32 possible colorings (legal and illegal)to color a graph with n vertices. The set of all possible colorings can be represented by a complete ternary tree called the search tree. In this tree,each path from the root to a leaf node represents one coloring assignment. ■ An incomplete coloring of a graph is partia/if no two adjacent colored vertices have the same color. Backtracking works by generating the underlying tree one node at a time. If the path from the root to the current node corresponds to a legal coloring,the process is terminated (unless more than one coloring is desired)

The 3-Coloring Problem ◼ There are 3n possible colorings (legal and illegal) to color a graph with n vertices. ◼ The set of all possible colorings can be represented by a complete ternary tree called the search tree. In this tree, each path from the root to a leaf node represents one coloring assignment. ◼ An incomplete coloring of a graph is partial if no two adjacent colored vertices have the same color. ◼ Backtracking works by generating the underlying tree one node at a time. ◼ If the path from the root to the current node corresponds to a legal coloring, the process is terminated (unless more than one coloring is desired)

The 3-Coloring Problem If the length of this path is less than n and the corresponding coloring is partial,then one child of the current node is generated and is marked as the current node. If,on the other hand,the corresponding path is not partial,then the current node is marked as a dead node and a new node corresponding to another color is generated. If,however,all three colors have been tried with no success,the search backtracks to the parent node whose color is changed,and so on

The 3-Coloring Problem ◼ If the length of this path is less than n and the corresponding coloring is partial, then one child of the current node is generated and is marked as the current node. ◼ If, on the other hand, the corresponding path is not partial, then the current node is marked as a dead node and a new node corresponding to another color is generated. ◼ If, however, all three colors have been tried with no success, the search backtracks to the parent node whose color is changed, and so on

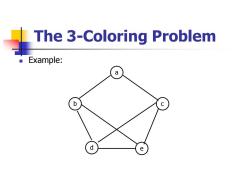
The 3-Coloring Problem Example: a b C d e

◼ Example: a The 3-Coloring Problem b c d e

The 3-Coloring Problem There are two important observations to be noted, which generalize to all backtracking algorithms: (1)The nodes are generated in a depth-first-search manner. (2)There is no need to store the whole search tree;we only need to store the path from the root to the current active node.In fact,no physical nodes are generated at all;the whole tree is implicit.We only need to keep track of the color assignment

The 3-Coloring Problem There are two important observations to be noted, which generalize to all backtracking algorithms: (1) The nodes are generated in a depth-first-search manner. (2) There is no need to store the whole search tree; we only need to store the path from the root to the current active node. In fact, no physical nodes are generated at all; the whole tree is implicit. We only need to keep track of the color assignment

The 3-Coloring Problem Recursive Algorithm Input:An undirected graph G=. Output:A 3-coloring d1...n]of the vertices of G,where each dil is 1,2,or 3. 1.for k-1to n 2.d←-0； 3.end for; 4.flagk-false; 5.graphcolor(1); 6.if fag then output c 7.else output "no solution"; graphcolor k) 1.for color作1to3 2.K←-color; 3.if cis a legal coloring then set fag<true and exit; 4. else if cis partial then graphcolor(k+1); 5,end for;

The 3-Coloring Problem Recursive Algorithm Input: An undirected graph G=(V, E). Output: A 3-coloring c[1…n] of the vertices of G, where each c[j] is 1, 2, or 3. 1. for k1 to n 2. c[k]0; 3. end for; 4. flagfalse; 5. graphcolor(1); 6. if flag then output c; 7. else output “no solution”; graphcolor(k) 1. for color=1 to 3 2. c[k]color; 3. if c is a legal coloring then set flag true and exit; 4. else if c is partial then graphcolor(k+1); 5. end for;

The 3-Coloring Problem Iterative Algorithm Input:An undirected graph G=,E). Output:A 3-coloring d1...]of the vertices of G where each di]is 1,2,or 3. 1.for k1 to n 2.d←-0； 3.end for; 4.fag-false; 5.k-1; 6.while 1 7. while d2 8. ①←+1； 9. if cis a legal coloring then set fag-true and exit from the two while loops; 10. else if cis partial then+1; 11. end while; 12. ←-0； 13. k-k1; 14.end while; 15.if fag then output c 16.else output "no solution";

The 3-Coloring Problem Iterative Algorithm Input: An undirected graph G=(V, E). Output: A 3-coloring c[1…n] of the vertices of G, where each c[j] is 1, 2, or 3. 1. for k1 to n 2. c[k]0; 3. end for; 4. flagfalse; 5. k1; 6. while k1 7. while c[k]2 8. c[k]c[k]+1; 9. if c is a legal coloring then set flagtrue and exit from the two while loops; 10. else if c is partial then kk+1; 11. end while; 12. c[k]0; 13. kk-1; 14. end while; 15. if flag then output c; 16. else output “no solution”;

The 8-Queens Problem How can we arrange 8 queens on an 8x8 chessboard so that no two queens can attack each other? Two queens can attack each other if they are in the same row,column or diagonal. The n-queens problem is defined similarly,where in this case we have n queens and an nxn chessboard for an arbitrary value of n1

The 8-Queens Problem ◼ How can we arrange 8 queens on an 88 chessboard so that no two queens can attack each other? ◼ Two queens can attack each other if they are in the same row, column or diagonal. ◼ The n-queens problem is defined similarly, where in this case we have n queens and an nn chessboard for an arbitrary value of n1