西安电子科技大学：《分析力学》课程教学资源（讲稿）第三章 能量原理及其应用

第三章能量原理及其应用(9) §3.1弹性体的功与应变能(2) §3.2虚功原理(1) §3.3单位载荷法(2) §3.4泛函与变分简介(1) §3.5最小势能原理(2) §3.6基于能量原理的近似解法(1)

第三章 能量原理及其应用(9) §3.1 弹性体的功与应变能(2) §3.2 虚功原理 (1) §3.3 单位载荷法 (2) §3.4 泛函与变分简介 (1) §3.5 最小势能原理 (2) §3.6 基于能量原理的近似解法 (1)

§3.1弹性体的功与应变能 ■当弹性体受到外力作用时，它就发生变形，因 而外力在变形位移方向上对弹性体做功。 ■如果不计及弹性体在加载和卸载时能量的损失 ，即当结构系统是保守系统，则对这样的物体 在变形时所做的功，可以看成是储存在物体中 的能量，称为应变能(strain energy)。因此， 应变能可以看成是弹性体变形时，它所吸收的 能量

 当弹性体受到外力作用时，它就发生变形，因 而外力在变形位移方向上对弹性体做功。  如果不计及弹性体在加载和卸载时能量的损失 ，即当结构系统是保守系统，则对这样的物体 §3.1 弹性体的功与应变能 ，即当结构系统是保守系统，则对这样的物体 在变形时所做的功，可以看成是储存在物体中 的能量，称为应变能（strain energy）。因此， 应变能可以看成是弹性体变形时，它所吸收的 能量

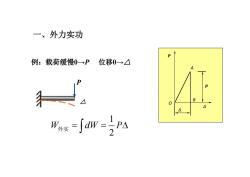
一、外力实功 例：载荷缓慢0→P 位移0△ B 0 W∫w-Pa

一、外力实功 P A P 例：载荷缓慢0→P 位移0→△ P Δ O B Δ P △ 1 2 W dW P 外实    

M A新 1 W外实 MO 2 外力实功：广义力与方向广义位移乘积的一半

 A y M 1 2 W M 外实   外力实功：广义力与方向广义位移乘积的一半

在线弹性范围内，外力由零开始缓慢增加到某一值， 将外力做的实功统一写成 1 W外实2 F△ 式中F一一广义力； △一一与广义力对应的位移，即为广义力作 用点且与广义力方向一致的位移。称为广义位 移

在线弹性范围内，外力由零开始缓慢增加到某一值， 将外力做的实功统一写成 式中 F——广义力； 1 = 2 W F 外实  Δ——与广义力对应的位移，即为广义力作 用点且与广义力方向一致的位移。称为广义位 移

若有一组力PP引起 P1 P2 P3 P4 各力作用点处的位移 414n △2 43 m外安=RA+2P4++P4+…+P4 =∑2A4=PY4 4是由P~P共同引起的位移 这一结论称为Clapeyron(克拉佩龙)定理

若有一组力P1 ~Pn引起 各力作用点处的位移 Δ1~Δn P1 P2 P3 P4 Δ1 Δ2 Δ3 Δ4     1 1  W P  P  Pii Pnn 2 1 2 1 2 1 2 1 外实  1 1  2 2   i 是由P1 ~Pn共同引起的位移 这一结论称为Clapeyron（克拉佩龙）定理。     T Pi i P 2 1 2 1  

应变能定理(Clapeyron定理)：如果线弹性 体在无限缓慢加载的条件下，始终处于平 衡状态时，弹性体内的应变能等于在变形 过程中外力所作的功

应变能定理(Clapeyron定理) ：如果线弹性 体在无限缓慢加载的条件下，始终处于平 衡状态时，弹性体内的应变能等于在变形 过程中外力所作的功

二、内力实功 若把弹性体看成许多微段，则它所接受的功等于外力（包括 外载荷和内力)在微段位移（包括刚体位移和变形位移）上所 作的功 由于微段所受力为平衡力系，平衡力系在微段的刚体位移 上不做功。因此若把弹性体看成许多微段，则它所接受的 功等于外力（包括外载荷和内力）在微段变形位移上所作的功

二、内力实功 若把弹性体看成许多微段，则它所接受的功等于外力(包括 外载荷和内力)在微段位移(包括刚体位移和变形位移)上所 作的功 由于微段所受力为平衡力系，平衡力系在微段的刚体位移 上不做功。因此若把弹性体看成许多微段，则它所接受的 功等于外力(包括外载荷和内力)在微段变形位移上所作的功

分布外力和集中外力在微段的变形上做功为高阶小量， 原因： 根据小变形假设，位移是一阶微量，因此微段变形为二阶微量 (1)内力在变形上做功为有限量乘以二阶微量，是二阶微量，但在 整个变形体内积分后，变为一阶微量；(2)集中力在变形上做功为 有限量乘以二阶微量，但只是有限个点，因此总和还是二阶微量， 可以忽略。(3)分布力在变形上做功为一阶微量乘以二阶微量，为 三阶微量，积分后为二阶微量，可以忽略。 因此若把弹性体看成许多微段，则它所接受的功等于内力 在微段变形位移上所作的功，即内力实功

分布外力和集中外力在微段的变形上做功为高阶小量， 原因： 根据小变形假设，位移是一阶微量，因此微段变形为二阶微量 （1）内力在变形上做功为有限量乘以二阶微量，是二阶微量，但在 整个变形体内积分后，变为一阶微量；（2）集中力在变形上做功为 有限量乘以二阶微量，但只是有限个点，因此总和还是二阶微量 ， 可以忽略。（3）分布力在变形上做功为一阶微量乘以二阶微量，为 三阶微量 ，积分后为二阶微量，可以忽略。 因此若把弹性体看成许多微段，则它所接受的功等于内力 在微段变形位移上所作的功,即内力实功

Me d

dx N N QM N N dx dλ Mdθ Q d η