福建船政交通职业学院：《机械设计基础》课程教学课件（PPT讲稿）单元二 常用机械机构 04 平面连杆机构

单元二常用机械机构 4平面连杆机构 S4.1概述 §4.2 平面机构的运动分析 §4.3平面机构的力分析 S4.4四杆机构的基本形式及其演化 §4.5平面四杆机构的基本特性 §4.6平面四杆机构的设计

§4.1 概述 §4.2 平面机构的运动分析 §4.3 平面机构的力分析 §4.4 四杆机构的基本形式及其演化 §4.5 平面四杆机构的基本特性 §4.6 平面四杆机构的设计 4 平面连杆机构 单元二 常用机械机构

4.1概述 平面连杆机构是由若干个构件通过低副联接而成的机构，又称为平面低 副机构。 由四个构件通过低副联接而成的平面连杆机构，称为四杆机构。 如果所有低副均为转动副，这种四杆机构就称为铰链四杆机构。 平面连杆机构的优点 ■由于是低副，为面接触，所以承受压强小、便于润滑、磨损较轻，可 承受较大载荷 ■结构简单，加工方便，构件之间的接触是有构件本身的几何约束来保 持的，所以构件工作可靠 ■可使从动件实现多种形式的运动，满足多种运动规律的要求 ■利用平面连杆机构中的连杆可满足多种运动轨迹的要求 平面连杆机构的缺点 ■根据从动件所需要的运动规律或轨迹来设计连杆机构比较复杂，精度不高。 ■运动时产生的惯性难以平衡，不适用于高速场合

4.1 概述 平面连杆机构是由若干个构件通过低副联接而成的机构，又称为平面低 副机构。 由四个构件通过低副联接而成的平面连杆机构，称为四杆机构。 如果所有低副均为转动副，这种四杆机构就称为铰链四杆机构。 平面连杆机构的优点 由于是低副，为面接触，所以承受压强小、便于润滑、磨损较轻，可 承受较大载荷 结构简单，加工方便，构件之间的接触是有构件本身的几何约束来保 持的，所以构件工作可靠 可使从动件实现多种形式的运动，满足多种运动规律的要求 利用平面连杆机构中的连杆可满足多种运动轨迹的要求 平面连杆机构的缺点 根据从动件所需要的运动规律或轨迹来设计连杆机构比较复杂，精度不高。 运动时产生的惯性难以平衡，不适用于高速场合

4.2平面机构的运动分析 机构的运动分析：已知机构中主动件的运动，求解机构中其他各构件的运 动状态。 通过机构的运动分析可了解机构在运动过程中构件上某些点的位移、 速度和加速度以及构件的角位移、角速度和角加速度。 本节主要介绍用相对运动图解法求机构的速度和加速度的方法

4.2 平面机构的运动分析 已知机构中主动件的运动，求解机构中其他各构件的运 动状态。 机构的运动分析： 通过机构的运动分析可了解机构在运动过程中构件上某些点的位移、 速度和加速度以及构件的角位移、角速度和角加速度。 本节主要介绍用相对运动图解法求机构的速度和加速度的方法

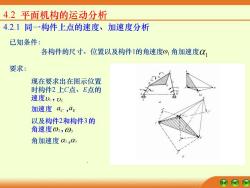
4.2平面机构的运动分析 4.2.1同一构件上点的速度、加速度分析 已知条件： 各构件的尺寸、位置以及构件1的角速度0，角加速度0心1 要求： 现在要求出在图示位置 时构件2上C点、E点的 速度De,DE 加速度ac,aE 以及构件2和构件3的 角速度02，⊙ 角加速度

4.2.1 同一构件上点的速度、加速度分析 已知条件： 各构件的尺寸、位置以及构件1的角速度 1 角加速度 1 要求： 、 现在要求出在图示位置 时构件2 上C点、E点的 速度 C ，  E 加速度 aC ， E a 以及构件2和构件3 的 角速度 2 ， 3 角加速度 2 ， 3 4.2 平面机构的运动分析

4.2平面机构的运动分析 1.速度分析 (1)求UB)B=OL4B,方向垂直于AB,指向与D的转向一致。 (2)求Uc B点与C点同为构件2上的点，根据理论力学，做平面 运动的刚体上某一点的速度可以看作是刚体上任选基点 的牵连速度和该点绕基点的相对转动速度的合成。因此 构件2上C点的速度等于B点的速度与C点相对B点的 速度矢量和，即 Vc DE UCB 大小 @lA ? 方向 ⊥CD ⊥AB ⊥BC

4.2 平面机构的运动分析 1.速度分析 （1）求  B  B =1l AB ，方向垂直于AB，指向与 1 的转向一致。 （2）求 C B 点与 C 点同为构件 2 上的点，根据理论力学，做平面 运动的刚体上某一点的速度可以看作是刚体上任选基点 的牵连速度和该点绕基点的相对转动速度的合成。因此 构件 2 上 C 点的速度等于B 点的速度与 C 点相对 B 点的 速度矢量和，即 C =  B + CB 大小 方向 ⊥CD ⊥ AB ⊥ BC ？ 1l AB ？

4.2平面机构的运动分析 构件1与构件2在B点组成转动副，所以Da,=DA，同理)c,=UC, 因此上式中只有两个未知数，可以用矢量多边形来求解。 ①如图所示，选定速度比例尺，(m/s/mm),任取极点p作矢量pb⊥AB, pb指向同o的转向一致，长度 pb=,这样矢量Db可以代表心。 M ②从b点作Us的方向线bc⊥BC 从p点作Uc的方向线pcL CD并交于c点 矢量pc代表Ue,矢量bc代表Um Ue=L•pc UcB=L,·bc

4.2 平面机构的运动分析 构件1与构件2在B点组成转动副，所以  B2 =  B1 ， 同理  C3 = C2 因此上式中只有两个未知数，可以用矢量多边形来求解。 ① 如图所示，选定速度比例尺为  (m/s/mm) ，任取极点p作矢量 pb ⊥ AB ， pb 指向同 1 的转向一致，长度   B pb = 这样矢量 pb 可以代表  B ②从b点作 CB 的方向线bc ⊥ BC 从ｐ点作 C 的方向线pc ⊥ 矢量 pc 代表 C ，矢量 bc 代表 CB C =  • pc  CB =  •bc  ， CD并交于c点

4.2平面机构的运动分析 (3)求020由图4.1可知 02= UCB 将矢量b移到机构简图中的C点处，则可见O2为逆时针方向。 o-么 将矢量pc移到机构简图中的C点处，则可见O,为逆时针方向。 (4)求)E因为B、C、E为同一构件上的点，所以可得出下列方程式： UE=UB VEB Uc UEC 大小？OlB ? L·PC 方向？ ⊥AB ⊥BE ⊥CD ⊥EC

4.2 平面机构的运动分析 （3）求 2 3 由图4.1可知 l BC  CB  = 2 将矢量 bc 移到机构简图中的C点处，则可见 2 为逆时针方向。 lCD C  = 3 将矢量 pc 移到机构简图中的C点处，则可见 3 为逆时针方向。 （4）求  E 因为B、C、E为同一构件上的点，所以可得出下列方程式：  E  B = + EB = C +  EC 大小 1l AB ？  • PC ？  ？ 方向 ？ ⊥ AB ⊥ BE ⊥CD ⊥ EC

4.2平面机构的运动分析 后一个方程只有两个未知数，可用图解法求解 如图4.1b所示，过b点作)EB 的方向线be⊥BE,过c点作 Uc的方向线ce⊥CE,两线交于e点 矢量pe代表D其大小为 Og=l,°pe ©a

4.2 平面机构的运动分析 后一个方程只有两个未知数，可用图解法求解 如图4.1b所示，过b点作 EB 的方向线 be ⊥ BE ，过c点作  EC 的方向线 ce ⊥CE ，两线交于e点 矢量 pe 代表  E 其大小为  E =  • pe 

4.2平面机构的运动分析 2.加速度分析 (1)求CB由已知条件可知：0B=oLAB方向为B→ACB=01lB 方向垂直于AB,指向与01方向一致。 (2)求0c 根据相对运动原理，可建立如下方程式 dc +ac dn +as +dce +dc 大小 wileD ilxn alA8 Q2IB 方向C→D ⊥CDB→A⊥ABC→B⊥BC 式中有两个未知数，可用矢量图解法求解

4.2 平面机构的运动分析 2.加速度分析  n B  n （ B = 1 l AB 1）求 B 由已知条件可知： = l AB 2 1 方向为B→ A 方向垂直于AB，指向与 1 方向一致。 式中有两个未知数，可用矢量图解法求解 （2）求  C 根据相对运动原理，可建立如下方程式 a n C a t C + = a n B a t B + a n CB + a t CB + 大小  lCD 2 3 ？  l AB 2 1 1 l AB  l AB 2 2 ？ 方向 Ｃ→Ｄ ⊥ ＣＤ Ｂ→Ａ ⊥ ＡＢ Ｃ→Ｂ ⊥ ＢＣ

4.2平面机构的运动分析 如图C所示，选定加速度比例尺4。(m/s2/m)任取一点P'为极点，作矢量 p6∥AB其大小为pb=2,指向为B-4,这样矢量p5可以代表 接着从b作矢量6万⊥AB,长度为b'b=,指向与a1方向一致，则矢量 b万代表a6;再作C∥BC,指向为C→B,长度为bc=，失量 b'c代表了aB作cc⊥BC 作为as的方向线；从p'作 pc”∥CD,方向为C→D,长度为 pc光，矢量pC代表 过c"作c"c⊥CD,作为 的方向线，与c"c'线相交于c

4.2 平面机构的运动分析 p b// AB ，其大小为 a n aB p b    = ( / / ) 任取一点P′为极点，作矢量 2 如图C所示，选定加速度比例尺 a m s mm ，指向为B→A，这样矢量 p b 可以代表 接着从b″作矢量 bb ⊥ AB ，长度为 a t B a b b    = ，指向与α1方向一致，则矢量 bb 代表 ；再作 b c // BC ，指向为C→B，长度为 a n CB a b c    = ，矢量 b c  t B a 代表了 n CB a c  c  ⊥ BC 作为 t aCB 的方向线；从p′作 作 p  c //CD ，方向为C→D，长度为 a n a c p c    = ，矢量 p  c  代表 n C a 过 c  作 c  c  ⊥ CD ，作为 t C a 的方向线，与 c  c  线相交于c′