中国科学技术大学：《计算机视觉》课程教学资源（PPT课件讲稿）第二章 视觉的基本知识 第三节 视觉系统的几何特性

第三节视觉系统的几何特性

第三节 视觉系统的几何特性

在任何特定的理论中，只有其中包 含数学的部分才是真正的科学。 康德

在任何特定的理论中，只有其中包 含数学的部分才是真正的科学。 ——康德

相关的数学基础 ▣齐次坐标 口射影几何 ▣2D变换 ▣3D变换 ▣相机内参数

相关的数学基础  齐次坐标  射影几何  2D变换  3D变换  相机内参数

1.齐次坐标 1、点的齐次坐标 二个齐次坐标如相差一个非零因子，则这二 个齐次坐标相同 2、无穷远直线上的点 如点 为无穷远直线上的点， 则t=0

1、点的齐次坐标 二个齐次坐标如相差一个非零因子，则这二 个齐次坐标相同             →       1 v u v u 2、无穷远直线上的点 如点 为无穷远直线上的点， 则 t =0           t v u 1. 齐次坐标

1.齐次坐标 3、直线的齐次坐标表示=(a,b,c 直线方程可表示为 z.i=ax+by+c=0. 规范化直线参数向量后，直线的齐次坐标可表示为： l=(位，立y,d=(位，d)with=1 i=(位r,ig）=(cos9,sin0)

3、直线的齐次坐标表示 直线方程可表示为 规范化直线参数向量后，直线的齐次坐标可表示为： 1. 齐次坐标

1.齐次坐标 4、通过二点的直线 4 如果 X1= 为三图象点，则通过 该二点的直线的参数向量为：L=X1×x2 x=0 Ix2=0 X2

4、通过二点的直线 如果 为二图象点，则通过 该二点的直线的参数向量为： 1 2 1 1 2 2 1 2 , u u x v x v t t         = =             1 2 L = x  x L x1 = 0 L x2 = 0 T T L x1 x2 1. 齐次坐标

1.齐次坐标 5、平行线可以相交 笛卡尔坐标系下，两条直线的方程为： Ax+By+C=0 Ax+By+D=0 齐次坐标系下，两条直线的方程为： A不+B上+C=0 w w Ax+By+Cw=0 A+B上+D=0 Ax+By+Dw=0 w w 可以解出w=0,即两条直线相交于无穷远点

5、平行线可以相交 1. 齐次坐标 笛卡尔坐标系下，两条直线的方程为： 齐次坐标系下，两条直线的方程为： 可以解出w=0，即两条直线相交于无穷远点

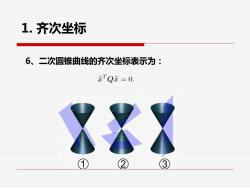
1.齐次坐标 6、二次圆锥曲线的齐次坐标表示为： 元Q元=0 ① 2 3

6、二次圆锥曲线的齐次坐标表示为： 1. 齐次坐标

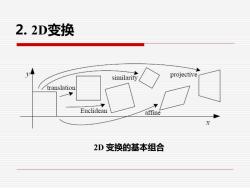
2.2D变换 similarity projective translation Euclidean affine 2D变换的基本组合

2. 2D变换 2D 变换的基本组合

2D变换 2D平移变预可猫述为： ] 或者： 2D旋转、平移变换可描述为： R t R= cos0 sin sin A cos 0

2D变换 2D平移变换可描述为： 或者： 2D旋转、平移变换可描述为：