厦门大学：《结构化学 Structural Chemistry》课程教学资源（电子教案）Chapter 03 Molecular symmetry and symmetry point group

Chapter 3 Molecular symmetry and symmetry point group 1 Symmetry elements and symmetry operations >Symmetry exists all around us and many people see it as being a thing of beauty. >A symmetrical object contains within itself some parts which are equivalent to one another. >The systematic discussion of symmetry is called Some objects are more symmetrical than others

Chapter 3 Molecular symmetry and symmetry point group §1 Symmetry elements and symmetry operations ¾Symmetry exists all around us and many people see it as being a thing of beauty. ¾A symmetrical object contains within itself some parts which are equivalent to one another. ¾The systematic discussion of symmetry is called : Some objects are more symmetrical than others

Why do we study the symmetry concept? >The molecular configuration can be expressed more simply and distinctly. >The determination of molecular configuration is greatly simplified. >It assists giving a better understanding of the properties of molecules. >To direct chemical syntheses;the compatibility in symmetry is a factor to be considered in the formation and reconstruction of chemical bonds. 1.Symmetry elements and symmetry operations symmetry operation .A action that leaves an object the same after it has been carried out is called symmetry operation. Example: Any rotation of sphere around axis through center brings sphere over into itself

¾ The molecular configuration can be expressed more simply and distinctly. ¾The determination of molecular configuration is greatly simplified. ¾It assists giving a better understanding of the properties of molecules. ¾To direct chemical syntheses; the compatibility in symmetry is a factor to be considered in the formation and reconstruction of chemical bonds. Why do we study the symmetry concept? symmetry operation •A action that leaves an object the same after it has been carried out is called symmetry operation. Any rotation of sphere around axis through center brings sphere over into itself Example: 1. Symmetry elements and symmetry operations

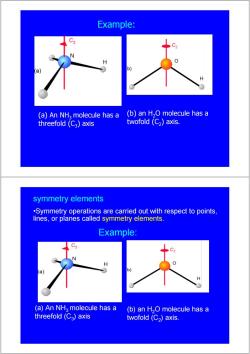
Example: (a)An NH2 molecule has a (b)an H2O molecule has a threefold (C3)axis twofold (C)axis. symmetry elements .Symmetry operations are carried out with respect to points, lines,or planes called symmetry elements. Example: (a)An NHa molecule has a (b)an H2O molecule has a threefold(Ca)axis twofold (C2)axis

(b) an H2O molecule has a twofold (C2) axis. (a) An NH3 molecule has a threefold (C3) axis Example: (b) an H2O molecule has a twofold (C2) axis. (a) An NH3 molecule has a threefold (C3) axis Example: •Symmetry operations are carried out with respect to points, lines, or planes called symmetry elements. symmetry elements

Symmetry elements 03 Some of the symmetry elements of a cube, the twofold,threefold,and fourfold axes. Symmetry Operation Symmetry operations are: Rotation Reflection nversion 60I UOI2LSAUI The corresponding symmetry elements are: aa如e a point

Some of the symmetry elements of a cube, the twofold, threefold, and fourfold axes. Symmetry elements Symmetry operations are: The corresponding symmetry elements are:

1)The identity (E) Operation by the identity operator leaves the molecule unchanged. All objects can be operated upon by the identity operation. Br 2)Inversion and the inversion center (i) .An object has a center of inversion,i,if it can be reflected through a center to produce an indistinguishable configuration

I F Cl Br • Operation by the identity operator leaves the molecule unchanged. • All objects can be operated upon by the identity operation. 1) The identity (E) 2) Inversion and the inversion center (i) •An object has a center of inversion, i, if it can be reflected through a center to produce an indistinguishable configuration

For example F 0=C=0 S. These have a center of inversion i. H H These do not have a center of inversion. >Inverts all atoms through the centre of the object 1 6 Inversion 5 30 03 Center of inversion 6 >Its matrix representation -1 0 0 0 0 -x 0 -1 0 0 -1 0 y 0 0 -1 0 0

These do not have a center of inversion. These have a center of inversion i. For example ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − 0 0 1 0 1 0 1 0 0 ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ z y x z y x z y x i 0 0 1 0 1 0 1 0 0 ¾Its matrix representation ¾Inverts all atoms through the centre of the object

3)Rotation and the n-fold rotation axis(C) Rotation about an n-fold axis (rotation through 360/n) is denoted by the symbol Cn. Example:Rotation of trigonal planer BFa 120°rotation 120°rotation F → B C3 -One three-fold(C3)rotation axes. (a=2元/3) The principle rotation axis is the axis of the highest fold The principle rotation axis is the axis of the highest fold. H

• Example: Rotation of trigonal planer BF3 C3 1 C3 2 Rotation about an n-fold axis (rotation through 360o/n) is denoted by the symbol Cn. 3) Rotation and the n-fold rotation axis (Cn) The principle rotation axis is the axis of the highest fold. –One three-fold (C3) rotation axes. (α=2π/3) C5 The principle rotation axis is the axis of the highest fold. C6

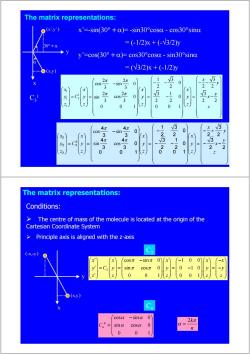
The matrix representations: o(xy) x'=-sin(30°+a)=-sin30°cosa-cos30°sina 30°+a =(-1/2)x+(-V3/2y y'=cos(30°+)=cos30°cosa-sin30°sind =(V3/2)x+(-1/2y (xy) 2π 2π 1 5 cos -sin 0 0 3 3 25 2 2 2 2 x x A N 2π sin 3 cos 3 0 y 0 x-x 2 2 y 0 0 0 0 1 4π 4π 1 3 3 cos sin 0 0 x 4 3 23 2 2 sin cos 0 0 x- 3 3 -20 y 2 2 z 0 0 1 1 The matrix representations: Conditions: > The centre of mass of the molecule is located at the origin of the Cartesian Coordinate System Principle axis is aligned with the z-axis C2 -snπ 0 0) -x sin 0 0 0 1 0 )(xy) cosa -sina 0 2kπ sin a cosa 0 0 0

The matrix representations: 30°＋α α （x,y） （x’,y’） C3 1 x y x’=-sin(30°＋α)= -sin30°cosα - cos30°sinα = (-1/2)x + (-√3/2)y y’=cos(30°＋α)= cos30°cosα - sin30°sinα = (√3/2)x + (-1/2)y ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − + = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ z y x y x z y x z y x z y x C z y x 2 2 3 2 3 2 0 0 1 0 2 1 2 3 0 2 3 2 1 0 0 1 0 3 4 3 4 0 3 4 3 4 2 3 2 2 2 π π π π sin cos cos sin 1 1 1 3 1 2 2 13 3 cos sin 0 0 3 3 2 2 22 2 2 31 3 cos cos 0 0 3 3 2 2 22 0 01 0 01 x y xx x x y y Cy y y x zz z z z π π π π ⎛ ⎞⎛ ⎞ ⎛ ⎞ − ⎜ ⎟⎜ ⎟ − − −− ⎜ ⎟ ⎛ ⎞ ⎛⎞ ⎛⎞ ⎛⎞ ⎜ ⎟ ⎜⎟ ⎜⎟ ⎜⎟ == = − =− ⎝ ⎠ ⎝⎠ ⎝⎠ ⎝⎠ ⎝ ⎠ ⎝ ⎠⎝ ⎠ sin ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 0 0 1 sin cos 0 cos sin 0 α α α α k Cn n kπ α 2 = 2 cos sin 0 1 0 0 sin cos 0 0 1 0 0 0 1 0 01 x x x xx y Cy y y y z z z zz π π π π ⎛ ⎞ ⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎛ ⎞⎛ ⎞ ⎛ ⎞ ′ − − − ⎜ ⎟ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ′ = = = − =− ′ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎝ ⎠⎝ ⎠ ⎝ ⎠ The matrix representations: C2 Cn （x,y） （-x,-y） x y Conditions: ¾ The centre of mass of the molecule is located at the origin of the Cartesian Coordinate System ¾ Principle axis is aligned with the z-axis

4)Reflection and the Mirror plane (o) >If reflection of an object through a plane produces an indistinguishable configuration then that plane is a plane of symmetry (mirror plane) denoted s. (x.y,-Z 6对 0 0 >There are three types of mirror planes: -If the plane is perpendicular to the vertical principle axis then it labeled on -If the plane contains the principle axis then it is labeled ov. -If a o plane contains the principle axis and bisects the angle between two adjacent 2-fold axes then it is labeled od

¾ If reflection of an object through a plane produces an indistinguishable configuration then that plane is a plane of symmetry (mirror plane) denoted s. 4) Reflection and the Mirror plane (σ) ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = 0 0 1 0 1 0 1 0 0 σ xy ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ z y x z y x z y x xy 0 0 1 0 1 0 1 0 0 σ （x, y,-z） z （x,y,z） y x ¾There are three types of mirror planes: ƒIf the plane is perpendicular to the vertical principle axis then it labeled σh. ƒIf the plane contains the principle axis then it is labeled σv. ƒIf a σ plane contains the principle axis and bisects the angle between two adjacent 2-fold axes then it is labeled σd

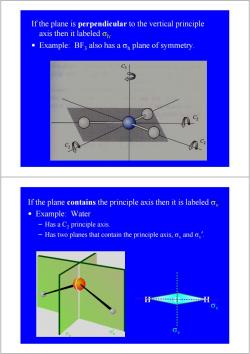
If the plane is perpendicular to the vertical principle axis then it labeled oh Example:BF3 also has a on plane of symmetry C3 9 C2 If the plane contains the principle axis then it is labeled o ● Example:Water Has a C2 principle axis. Has two planes that contain the principle axis,o,and o,. 6

If the plane is perpendicular to the vertical principle axis then it labeled σh. • Example: BF3 also has a σh plane of symmetry. If the plane contains the principle axis then it is labeled σv. • Example: Water – Has a C2 principle axis. – Has two planes that contain the principle axis, σv and σv ’. H H O σv σv