香港中文大学：《Topics in Theoretical Computer Science》课程教学资源（PPT课件讲稿）Lecture 10 Online learning. Expert problem

CMS57opomtr cine Week 10:Online Learning Instructor:Shengyu Zhang 1

Instructor: Shengyu Zhang 1

Location change for the final 2 classes Nov 17:YIA 404 (Yasumoto International Academic Park康本國祭學術園) ■Nov24:No class. Conference leave. Dec 1:YIA 508 (Yasumoto International Academic Park康本國祭學術園) 2

Location change for the final 2 classes ◼ Nov 17: YIA 404 (Yasumoto International Academic Park 康本國際學術園) ◼ Nov 24: No class. ❑ Conference leave. ◼ Dec 1: YIA 508 (Yasumoto International Academic Park 康本國際學術園) 2

Problem 1:Experts problem 3

Problem 1: Experts problem 3

Stock market StP 500 indixuekly 0边 -410购 000 00 050 Simplification:Only consider up or down. 4

Stock market ◼ Simplification: Only consider up or down. 4

Which expert to follow? Each day,stock market goes up or down. TRUSSKEY FINANCIAL ADVISORS Let'sTalk Investing N小d HERB WHITE TIAHOME.COM (936)588-0288 Each morning,n“experts'”predict the market.. How should we do?Whom to listen to?On combine their advice in some way? 5

Which expert to follow? ◼ Each day, stock market goes up or down. ◼ Each morning, 𝑛 “experts” predict the market. ◼ How should we do? Whom to listen to? Or combine their advice in some way? 5

Which expert to follow? Each day,stock market goes up or down. TRUSSKEY FINANCIAL ADVISORS Let's Talk Investing N小d HERB WHITE TIAHOME.COM (936)588-0288 At the end of the day,we'll see whether the market actually goes up or down. We lose 1 if our prediction was wrong. 6

Which expert to follow? ◼ Each day, stock market goes up or down. ◼ At the end of the day, we’ll see whether the market actually goes up or down. ◼ We lose 1 if our prediction was wrong. 6

After a year,we'll see with hindsight that one expert is the best. But,of course,we don't know who in advance. nWe''ll think“'If we had followed his advice.” Theorem:We have a method to perform close to the best expert! We don't assume anything about the experts. They may not know what they are talking about They may even collaborate in any bad manner

◼ After a year, we’ll see with hindsight that one expert is the best. ❑ But, of course, we don’t know who in advance. ◼ We’ll think “If we had followed his advice…” ◼ Theorem: We have a method to perform close to the best expert! ❑ We don’t assume anything about the experts. ◼ They may not know what they are talking about. ◼ They may even collaborate in any bad manner. 7

Method and intuition Algorithm:Randomized Weighted Majority Use random choice:following expert i with probability pi If an expert predicts wrongly:punish him by decreasing the probability of choosing him/her in next round. If someone gives you wrong info,then you tend to trust him less in future. 8

Method and intuition ◼ Algorithm: Randomized Weighted Majority ◼ Use random choice: following expert 𝑖 with probability 𝑝𝑖 ◼ If an expert predicts wrongly: punish him by decreasing the probability of choosing him/her in next round. ❑ If someone gives you wrong info, then you tend to trust him less in future. 8

Randomized Weighted Majority w:weight of experti at time :probability of choosing expertiat time for each i∈[n] w0=1,p=1/m for each t>1,i∈[n]: if expert i was wrong at step t-1 w0=w-(1-e) else Decrease your weight! w=w-0 op40=w0/∑w0 Probability is proportional to weight Choose i with prob.p and follow expert i's advice. 9

Randomized Weighted Majority ◼ for each 𝑖 ∈ [𝑛] 𝑤𝑖 (1) = 1, 𝑝𝑖 (1) = 1/𝑛 ◼ for each 𝑡 > 1, ∀𝑖 ∈ [𝑛]: ❑ if expert 𝑖 was wrong at step 𝑡 − 1 𝑤𝑖 (𝑡) = 𝑤𝑖 (𝑡−1) (1 − 𝜀) else 𝑤𝑖 (𝑡) = 𝑤𝑖 (𝑡−1) ❑ 𝑝𝑖 (𝑡) = 𝑤𝑖 𝑡 /σ𝑖 𝑤𝑖 (𝑡) ❑ Choose 𝑖 with prob. 𝑝𝑖 (𝑡) , and follow expert 𝑖’s advice. 𝑤𝑖 (𝑡) : weight of expert 𝑖 at time 𝑡 𝑝𝑖 (𝑡) : probability of choosing expert 𝑖 at time 𝑡 Decrease your weight! Probability is proportional to weight 9

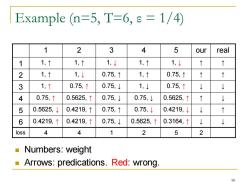
Example (n=5,T=6,e=1/4) 1 2 3 4 5 our real 1 1,↑ 1,↑ 1,↓ 1,↑ 1,↓ ↑ 2 1,↑ 1, 0.75,↑ 1,↑ 0.75,↑ 个 3 1,↑ 0.75,↑ 0.75,↓ 1,↓ 0.75,↑ ↓ 4 0.75,↑ 0.5625,↑ 0.75,↓ 0.75,↓ 0.5625,↑ 5 0.5625,↓ 0.4219,↑ 0.75,↑ 0.75,↓ 0.4219,↓ 6 0.4219,↑ 0.4219,↑ 0.75,↓ 0.5625,↑ 0.3164,↑ ↓ loss 4 4 1 2 5 2 Numbers:weight Arrows:predications.Red:wrong. 10

Example (n=5, T=6, ε = 1/4) 1 2 3 4 5 our real 1 1, ↑ 1, ↑ 1, ↓ 1, ↑ 1, ↓ ↑ ↑ 2 1, ↑ 1, ↓ 0.75, ↑ 1, ↑ 0.75, ↑ ↑ ↑ 3 1, ↑ 0.75, ↑ 0.75, ↓ 1, ↓ 0.75, ↑ ↓ ↓ 4 0.75, ↑ 0.5625, ↑ 0.75, ↓ 0.75, ↓ 0.5625, ↑ ↑ ↓ 5 0.5625, ↓ 0.4219, ↑ 0.75, ↑ 0.75, ↓ 0.4219, ↓ ↓ ↑ 6 0.4219, ↑ 0.4219, ↑ 0.75, ↓ 0.5625, ↑ 0.3164, ↑ ↓ ↓ loss 4 4 1 2 5 2 ◼ Numbers: weight ◼ Arrows: predications. Red: wrong. 10