上海交通大学：《Structural and Chemical Characterization of Materi》教学资源_crystallography

Crystallography Leyun Wang School of Materials Science and Engineering, SJTU leyunwang@sjtu.edu.cn 1

Crystallography Leyun Wang School of Materials Science and Engineering, SJTU leyunwang@sjtu.edu.cn 1

Crystallography ·Crystal systems and Bravais lattices(晶 系与布拉维点阵) 影 ·Point group and space group(点群 与空间群) 。Reciprocal lattice (倒易点阵)

Crystallography • Crystal systems and Bravais lattices ( 晶 系与布拉维点阵 ) • Point group and space group (点群 与空间群 ) • Reciprocal lattice (倒易点阵 ) 2

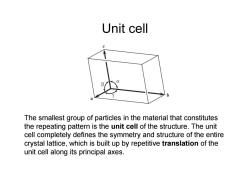
Unit cell a The smallest group of particles in the material that constitutes the repeating pattern is the unit cell of the structure.The unit cell completely defines the symmetry and structure of the entire crystal lattice,which is built up by repetitive translation of the unit cell along its principal axes

Unit cell The smallest group of particles in the material that constitutes the repeating pattern is the unit cell of the structure. The unit cell completely defines the symmetry and structure of the entire crystal lattice, which is built up by repetitive translation of the unit cell along its principal axes

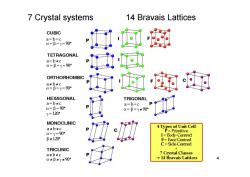
7 Crystal systems 14 Bravais Lattices CUBIC a=b=c =B=y=90° TETRAGONAL a=b+c =B=y=90° ORTHORHOMBIC a+b+c &=B=y=90° HEXAGONAL TRIGONAL a=btc a=b=c =B=90° =B=y*90° y=120° MONOCLINIC atb#c 4 Types of Unit Cell P=Primitive =y=90° I=Body-Centred B*120° F=Face-Centred C=Side Centred TRICLINIC a+b+c 7 Crystal Classes *阝*y*90° →14 Bravais Lattices 4

4 7 Crystal systems 14 Bravais Lattices

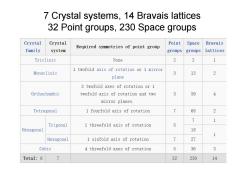
7 Crystal systems,14 Bravais lattices 32 Point groups,230 Space groups Crystal Crystal Point Space Bravais Required symmetries of point group family system groups groups lattices Triclinic None 2 2 1 1 twofold axis of rotation or 1 mirror Monoclinic 3 13 2 plane 3 twofold axes of rotation or 1 Orthorhombic twofold axis of rotation and two 3 59 4 mirror planes. Tetragonal 1 fourfold axis of rotation 7 68 2 7 1 Trigonal 1 threefold axis of rotation 5 Hexagonal 18 1 Hexagonal 1 sixfold axis of rotation 7 27 Cubic 4 threefold axes of rotation 5 36 3 Total:6 7 32 230 14

5 7 Crystal systems, 14 Bravais lattices 32 Point groups, 230 Space groups

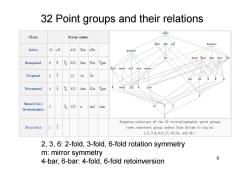
32 Point groups and their relations m3m Class Group names 43m432m3 6/mmm Cubic 23 m3 432 43m m3m 4/mmm 23 6mm6m26226/m3m Hexagonal 6 6 % 622 6mm 62m 42m 4mm 422 4/m mmm Trigonal 3 3 32 3m 3m 3m 32 Tetragonal 422 Amm 42m mm2 222 2/m Monoclinic 2 头 222 mm2 nunm Orthorhombic Subgroup relations of the 32 crystallographic point groups Triclinic y (rows represent group orders from bottom to top as: 1,2,3,4,6,8,12,16,24,and48.) 2,3,6:2-fold,3-fold,6-fold rotation symmetry m:mirror symmetry 6 4-bar,6-bar:4-fold,6-fold retoinversion

6 32 Point groups and their relations 2, 3, 6: 2-fold, 3-fold, 6-fold rotation symmetry m: mirror symmetry 4-bar, 6-bar: 4-fold, 6-fold retoinversion

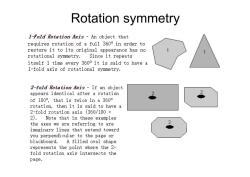
Rotation symmetry I-Fold Rotation Axis -An object that requires rotation of a full 3600 in order to restore it to its original appearance has no rotational symmetry. Since it repeats itself 1 time every 3600 it is said to have a 1-fold axis of rotational symmetry. 2-fold Rotation Axis If an object appears identical after a rotation of180°，that is twice in a360° rotation,then it is said to have a 2-fold rotation axis (360/180 = 2).Note that in these examples the axes we are referring to are imaginary lines that extend toward you perpendicular to the page or blackboard.A filled oval shape represents the point where the 2- fold rotation axis intersects the page

7 Rotation symmetry

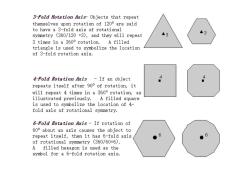
3-Fold Rotation Axis-Objects that repeat themselves upon rotation of 1200 are said to have a 3-fold axis of rotational symmetry (360/120 =3),and they will repeat 3 3 3 times in a 3600 rotation. A filled triangle is used to symbolize the location of 3-fold rotation axis. 4-Fold Rotation Axis -If an object ◆ repeats itself after 900 of rotation,it will repeat 4 times in a 3600 rotation,as illustrated previously.A filled square is used to symbolize the location of 4- fold axis of rotational symmetry. 6-Fold Rotation Axis-If rotation of 600 about an axis causes the object to repeat itself,then it has 6-fold axis 6 6 ● of rotational symmetry (360/60=6). A filled hexagon is used as the symbol for a 6-fold rotation axis

8

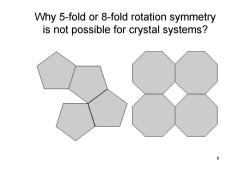
Why 5-fold or 8-fold rotation symmetry is not possible for crystal systems? 9

9 Why 5-fold or 8-fold rotation symmetry is not possible for crystal systems?

mirror symmetry E m

10 mirror symmetry