上海交通大学：《材料加工原理 Principles of Materials Processing》教学资源（课件讲稿）凝固和铸造 Solidification and casting_Solidification of single phase alloys（2）

先进材料疑固实验室 Laboratory of Advanced Materials Solidification 1896 1920 1987 2006 Solidification of single phase alloys(2) Dr.Mingxu Xia anced Maw 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY

1896 1920 1987 2006 Solidification of single phase alloys (2) Dr. Mingxu Xia

先进材料疑固实验室 OUTLINE Laboratory of Advanced Materials Solidification Solute Redistribution Solute distribution coefficient Solute redistribution in equilibrium state Solute redistribution in non-equilibrium state Solute distribution in front of S/L interface Application:Zone melting Morphology Instability of a S/L interface Constitutional undercooling Morphological instability of a S/L interface Interface instability of pure metal Solidification microstructure:Cells and dendrites nced Mav 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY

OUTLINE Solute Redistribution • Solute distribution coefficient • Solute redistribution in equilibrium state • Solute redistribution in non-equilibrium state • Solute distribution in front of S/L interface • Application: Zone melting Morphology Instability of a S/L interface • Constitutional undercooling • Morphological instability of a S/L interface • Interface instability of pure metal • Solidification microstructure: Cells and dendrites

先进材料疑固实验室 Situation 3:No diffusion in the solid,normal Laboratory of Advanced Materials Solidification diffusion in the liquid,no convection. In Situation 3,there exists a steady state in which the solid growth does not cause any change of the distribution of solute concentration in the liguid. y af IS S anced Materia 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY

In Situation 3, there exists a steady state in which the solid growth does not cause any change of the distribution of solute concentration in the liquid. Situation 3: No diffusion in the solid, normal diffusion in the liquid, no convection

先进材料疑固实验室 Situation 3:No diffusion in the solid,Limited diffusion in the liquid,no convection. Laboratory of Advanced Materials Solidification L Phase diagram T厂 C Initial point koCp C's Co C'L Colko 5 Solute concentration (b) L L Clk C Transient stage Steady state stage 5 (c) 5 (d) The figure is from 切聊过被阶段 稳定生长阶段 徐洲，姚寿山主编，《材料 8 mitial Steady 加工原理》科技出版社， transient state 最后过该阶段1 2003 stage. stage Final p62 8 transientL (e) stage 熟 上浒充通大 SHANGHAI JIAO TONG UNIVERSITY

Situation 3: No diffusion in the solid, Limited diffusion in the liquid, no convection

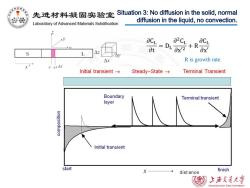
先进材料凝固实验室 Situation 3:No diffusion in the solid,normal diffusion in the liquid,no convection. Laboratory of Advanced Materials Solidification aCL at S L △x R is growth rate. rr+Ar Initial transient→ Steady-State→ Terminal Transient Boundary Terminal transient layer Initial transient start X dist ance finish 上游充通大学 SHANGHAI JIAO TONG UNIVERSITY

R is growth rate. Situation 3: No diffusion in the solid, normal diffusion in the liquid, no convection

先进材料疑固实验室 Situation 3:No diffusion in the solid,normal Laboratory of Advanced Materials Solidification diffusion in the liquid,no convection. To maintain the overall mass balance,Cs*must be equal to Co in the steady state. In the steady state,the concentration differential equation -D股 aCL t can be changed into: n器+ dCy二0 R growth rate x'=the distance of the point of interest from the solid/liquid interface D=diffusion coefficient of solute atom in the liquid. 上浒充通大 SHANGHAI JIAO TONG UNIVERSITY

To maintain the overall mass balance, CS* must be equal to C0 in the steady state. In the steady state, the concentration differential equation can be changed into: Situation 3: No diffusion in the solid, normal diffusion in the liquid, no convection. R = growth rate x’= the distance of the point of interest from the solid/liquid interface DL = diffusion coefficient of solute atom in the liquid

先进材料疑固实验室 Situation 3:No diffusion in the solid,normal Laboratory of Advanced Materials Solidification diffusion in the liquid,no convection. Characteristic equation of d2CL is D2+R1=0 Then =一 R 入1=0 The general solution CL Ciehx +C2eax Then nced Materials Sol G-G+Ge 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY

Situation 3: No diffusion in the solid, normal diffusion in the liquid, no convection. Characteristic equation of is Then The general solution Then

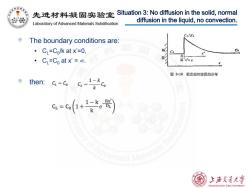
先进材料疑固实验室 Situation 3:No diffusion in the solid,normal diffusion in the liquid,no convection. Laboratory of Advanced Materials Solidification Co/Ka The boundary conditions are: ·C=Co/k at x'=0, x 。 CL=Co at x'=c0. 面x 图3-19稳定态时溶质的分布 then::c=-G-1产 c=c(+） anoedMaterialsSol 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY

The boundary conditions are: • CL=C0/k at x’=0, • CL=C0 at x’ = ∞. then: Situation 3: No diffusion in the solid, normal diffusion in the liquid, no convection

Situation 3:No diffusion in the solid,Limited 先进材料疑固实验室diffusion in the liquid,no convection. Laboratory of Advanced Materials Solidification At initial transient state,we assume the concentration variation rate of solid is linearly related to solid concentration: d(Cs-Co) dx' =-a(C-Cg) a-is the parameter for the linear relationship then Co-Cs Ae-ax Boundary condition:Cs=kCo at x'=0 ©It is obtained that: Cs=C[1-(1-ko)e-x2] 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY

At initial transient state, we assume the concentration variation rate of solid is linearly related to solid concentration: then Boundary condition: Cs=kC0 at x’=0 It is obtained that: Situation 3: No diffusion in the solid, Limited diffusion in the liquid, no convection. α- is the parameter for the linear relationship

Situation 3:No diffusion in the solid,Limited 先进材料疑固实验室diffusion in the liquid,no convection.. Laboratory of Advanced Materials Solidification The solute expelled from solid: (Co-C)ax' And the solute increased in liquid f(c-conax Then c-cds'-c Substitute C=C[1-(1-k)e-ae c=c0+'.) (in liquid,steady state as boundary condition) in to above equation 熟 上浒充通大 SHANGHAI JIAO TONG UNIVERSITY

The solute expelled from solid: And the solute increased in liquid Then Substitute in to above equation Situation 3: No diffusion in the solid, Limited diffusion in the liquid, no convection. (in liquid, steady state as boundary condition)