西安电子科技大学：《离散数学》课程教学课件（题解）第四章 函数与无限集合 4-1 函数

西安电子科技大学离散数学软件学院第二篇集合论第4章函数与无限集合第21课时4.1函数的概念?第22课时4.2逆函数和复合函数第23课时4.3可数与不可数集合第24课时4.4集合基数的比较

西安电子科技大学 离散数学 软件学院 第二篇 集合论 第21课时 4.1 函数的概念 第4章 函数与无限集合 4.3 可数与不可数集合 4.2 逆函数和复合函数 4.4 集合基数的比较 第22课时 第23课时 第24课时

西安电子科技大学函数的定义$4.1.1软件学院家家家设X和Y是集合，是从X到Y上的二元关系，函数如果对于每一个xEX都有唯一的yEY，使得Ef，称为从X到Y的函数，记为：X一Y。函数又称作映射或变换。函数的形式定义J :X-Y(Vx)(xEX-(Fy)(yEYAE J -y-z)函数区别于一般二元关系的两个特点：（1）函数的定义域等于前域：（2）对于前域每个元素，陪域中仅有唯一的一个象与之对应

西安电子科技大学 函数的定义 软件学院 函数 §4.1.1 函数的形式定义 函数区别于一般二元关系的两个特点： （1）函数的定义域等于前域； （2）对于前域每个元素，陪域中仅有唯一的一个象与之对应

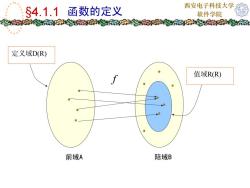
西安电子科技大学函数的定义$4.1.1软件学院定义域D(R)值域R(R)前域A陪域B

西安电子科技大学 软件学院 值域R(R) 定义域D(R) 前域A 陪域B §4.1.1 函数的定义 f

西安电子科技大学函数的定义$5.1.1软件学院家家设为从集合X到Y的函数，任取xEX，象若Ef，则称y为在f作用下x的映象（简称象），记为f(x)=y，而x则称为y的原象。若XCX，称f(X)=f（x）IXEX为函数f下X的映象。特别地，称整个前域的映象f（X）为函数的值域

西安电子科技大学 函数的定义 软件学院 象 §5.1.1

西安电子科技大学函数的定义$4.1.1软件学院（例题）判断下列关系中哪些能构成函数(a) =(x1,X2EN,XI+x2/y1, y2ER,y2=y1)（c）=(X1X2EN，x2为小于x1的素数个数）解答：(a）不能，因为D(）N，且每个1对应多个。（b）不能，一个y1对应多个y2.（c）能。因为D(f)=N，且对每个x1EN，都有唯一的元素x2EN与之对应

西安电子科技大学 §4.1.1 函数的定义 软件学院 【例题】判断下列关系中哪些能构成函数 解答：

西安电子科技大学函数的定义$4.1.1 i软件学院教家家家【思考题】设A和B都是有限集合，且有|A|=m，|B|=n。问A到B上有多少个不同的函数？解答：设函数f :A→B，A={ai,a2,"",amj,可以将f表示为以下模板：f ={,,",,}其中每个位置可用B中任意元素替换。这样不同的组合共有nm种因此，A到B可以定义nm个不同的函数

西安电子科技大学 §4.1.1 函数的定义 软件学院 【š思考题】设A和B都是有限集合，且有|A|=m, |B|=n。问 A到B上有多少个不同的函数？ 设函数f :A→B，A={a1,a2,.,am}, 可以将f 表示为以下模板： f ={, , .,, } 其中每个□位置可用B中任意元素替换。 解答： m m 这样不同的组合共有nm种。 因此，A到B可以定义nm个不同的函数

西安电子科技大学特殊函数类$4.1.2软件学院家设f是从集合X到Y的函数。特殊函数类（a）若任取yEY，存在xEX，使得f(x)=y，则称f为满射（到上映射）（b）任取xl，x2EX，如果X,，，那么f(x)(），则称为为单射（内射、入射、一对一映射)。（c）若f既是单射又是满射，则f为双射（对应的映射）

西安电子科技大学 软件学院 特殊函数类 §4.1.2 特殊函数类

西安电子科技大学$4.1.2特殊函数类软件学院TXVx,y EX, 若x≠y则f(x)±f(y)单射fVyEY,3xEX，满足f(x)=y满射X既是单射又是满射双射

西安电子科技大学 软件学院 f f f 单射 满射 双射 ∀x,y∈X, 若x≠y则f(x)≠f(y) X Y X Y X Y ∀y∈Y, ∃x∈X ，满足f(x)=y 既是单射又是满射 §4.1.2 特殊函数类

西安电子科技大学特殊函数类$4.1.2软件学院家办【例题】判断下列函数的类型(a) s:N-N, s(n)-n+l;(b)h:R-R，(x)=x3+2x2(c) a, beR 且 ab, g:[0, 1]-[a, b], g(x)-(b-a)x+a解答：（a）s是单射而非满射：（b）h是满射而非单射：（c）g是双射

西安电子科技大学 §4.1.2 特殊函数类 软件学院 解答：

西安电子科技大学特殊函数类$4.1.2 软件学院茶家教家家「定理」设f是从集合X到Y的函数。（a）若f是满射的，则必有IXI≥IYI：（b）若f是单射的，则必有IXI≤IYI；（c）若f为双射，则必有IXI=IYI;（d）若IXI=IYI，则有f是单射的当且仅当f是满射的

西安电子科技大学 §4.1.2 特殊函数类 软件学院