华东理工大学:《信号与系统》课程教学资源(课件讲稿)第五章 拉普拉斯变换和连续时间系统的复频域分析(1/2)

Ch5 拉普拉斯变换和连续时间系统的 Laplace Transform 复频域分析 本章要点 •拉氏变换的定义一从傅立叶变换到拉氏 变换 拉氏变换的收敛域,性质 ·系统函数和单位冲激响应 S域分析、极点与零点 频率响应,稳定性分析 •信号流图与系统模拟 拉氏变换与傅氏变换的关系
1 Ch5 拉普拉斯变换和连续时间系统的 复频域分析 本章要点 •拉氏变换的定义——从傅立叶变换到拉氏 变换 •拉氏变换的收敛域,性质 •系统函数和单位冲激响应 •S域分析、极点与零点 •频率响应,稳定性分析 •信号流图与系统模拟 •拉氏变换与傅氏变换的关系 Laplace Transform

Recall:上一章讲述了F-变换:ff0emd F-变换是将信号表示成复指数e线性组合,s=jo F-变换在信号分析(频谱)及LTI系统分析(频响特性) 具有非常重要的作用,而信号与系统之相互作用可由卷 积定理方便表述。 同时注意到F-变换侧重于信号分析 2
2

C变换: 作为F-变换的推广,也是将信号表示成复指数e线性组 合,其中s为任意复数5=o+j0。L-变换除了和F变换一样 分析信号与乩T1系统,同时提供了研究信号与系统的另一种 工具,更重要的是C变换还可以用来分析F-变换所不能分 析的系统,如不稳定系统。 因此要注意 变换侧重于系统分析 3
3

本章重点: -变换在系统分析中应用,如系统函数的概念、系 统时域特性、系统频域特性、系统稳定性分析等。 本章思路: 变换定义、性质→结合系统分析介绍变换的应用 4
4

5.1.1 Definition-from FT to LT 有几种情况不满足狄里 。 若乘一衰减因子e -ot 赫利条件: 石为任意实数,则 f(t).e-a 收敛,于 是满足狄里赫利条件 ·u() u(t)eo 增长信号e(a>0) 周期信号c0S01t (o>a) e-ai cos t 5
5 5.1.1 Definition——from FT to LT 有几种情况不满足狄里 赫利条件: • u(t) • 增长信号 • 周期信号 e (a 0) at • 若乘一衰减因子 为任意实数,则 收敛,于 是满足狄里赫利条件 , t e t f t e ( ). t u t e ( ) e .e ( a) at t e t t 1 cos t 1 cos

因果 f(t)=f(t)e S=0+j0 F()=f(t)e-dt 象函数 正LT F(s)=f(t)e-"dt 反变换 fe"=2 F (0 )e i'do (eed )S=0+j@ 原函数 逆LT F(s)e"ds ds=jdo FT:实频率 是振荡频率 LT复频率S 是振荡频率, 控制衰减速度 6
6 t f t f t e ( ) ( ) 1 F f t e dt j t 0 ( ) 1 ( ) ( ) 因果 0 F(s) f (t)e dt st sj 象函数 正LT F s e ds j f t j j st ( ) 2 1 ( ) 原函数 逆LT FT: 实频率 是振荡频率 LT: 复频率S 是振荡频率, 控制衰减速度 f t e F e d t j t ( ) 2 1 ( ) 1 f t F e e d t j t ( ) 2 1 ( ) 1 反变换 ds jd s j

单边拉式正变换: Unilateral LT F(s)=f()e-"dt=LTIf(t)] 单边拉式反变换: F(s)est ds ].u(t)=LT[F(S)] Jo-jo 双边拉式正变换: F,(s)=[f(t)e-"dt Bilateral LT 双边拉式反变换: f(t)= F(s)e"ds 2元jJo-j0 7
7 ( ) ( ) [ ( )] 0 F s f t e dt LT f t st ( ) ] ( ) [ ( )] 2 1 ( ) [ 1 F s e ds u t LT F S j f t j j st 单边拉式正变换: 单边拉式反变换: F s f t e dt st b ( ) ( ) F s e ds j f t j j st b ( ) 2 1 ( ) 双边拉式正变换: 双边拉式反变换: Bilateral LT Unilateral LT

5.1.2收敛条件 Region of Convergence 在S复平面中,凡能使F(S)存在的S值的范 围称为拉式变换的收敛域(ROC) 1.单边拉式变换的收敛域 lim f(t)e-=0 (> t→0 若上式在σ>o,时成立,则函数f)的拉式变换在 ReS]>o,的范围内是收敛域的。 收敛域:s时右侧的阴影部分ReS>o的范围。 收敛轴:σ=o时的直线, 收敛边界 收敛坐标:oo 8
8 5.1.2 收敛条件 在S复平面中,凡能使F(S)存在的S值的范 围称为拉式变换的收敛域(ROC)。 0 a j lim ( ) 0 ( ) 0 t t f t e 1. 单边拉式变换的收敛域 若上式在>0时成立,则函数 f(t) 的拉式变换在 Re[S] >0的范围内是收敛域的。 收敛域:0时右侧的阴影部分 Re[S] >0的范围。 收敛轴: =0时的直线, 收敛边界 收敛坐标: 0 Region of Convergence
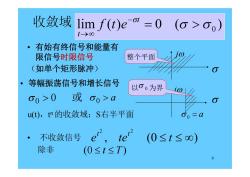
收敛域 limf(t)eo=0(o>oo) 有始有终信号和能量有 限信号时限信号 整个平面 (如单个矩形脉冲) 等幅振荡信号和增长信号 以00为界 o0>0或o0>a u(),n的收敛域:S右半平面 不收敛信号 e, te (0≤t≤oo) 除非 (0≤t≤T) 9
9 lim ( ) 0 ( ) 0 t t 收敛域 f t e • 有始有终信号和能量有 限信号时限信号 (如单个矩形脉冲) 0 0 或 a 0 , (0 ) 2 2 e te t t t 整个平面 j 0 a 以 0 为界 j (0 t T) • 等幅振荡信号和增长信号 • 不收敛信号 除非 u(t),t n 的收敛域:S右半平面
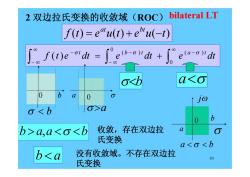
2双边拉氏变换的收敛域(ROC) bilateral LT f(1)=e"u(t)+eu(-t) f(t)e-aldi -e-aydt+ed oa 0 b b>a,a<o<b 收敛,存在双边拉 a 氏变换 a<o<b b<a 没有收敛域。不存在双边拉 10 氏变换
10 f (t) e u(t) e u( t) at bt 0 ( ) 0 ( ) f (t)e dt e dt e dt t b t a t b a ba,a b b a 收敛,存在双边拉 氏变换 没有收敛域。不存在双边拉 氏变换 2 双边拉氏变换的收敛域(ROC) 0 b b 0 a a 0 b a b j a bilateral LT
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第四章 傅立叶变换在系统分析中的应用(2/2).pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第四章 傅立叶变换在系统分析中的应用(1/2).ppt
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第三章 傅里叶变换 §3.8 Fourier transform of sampling signals(抽样信号).pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第三章 傅里叶变换 §3.9 Fourier transform of periodic signal(周期FT).pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第三章 傅里叶变换 §3.5 傅里叶变换的性质 Properties of Fourier Transform.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第三章 傅里叶变换 §3.4 常用非周期信号的频谱.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第三章 傅里叶变换 §3.2 非周期信号的傅立叶变换.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第三章 傅里叶变换 3.1 Frequency analysis of periodic signals(FS).pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第二章 连续时间系统的时域分析方法.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)信号的分解.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第一章 信号与系统概述.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)常见基本信号、奇异信号 Singularity signals.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)绪论 Signals and Systems(任课教师:朱煜).pdf
- 华东理工大学:《信号与系统》课程教学资源(试卷习题)各章习题(含解答).pdf
- 华东理工大学:《信号与系统》课程教学资源(试卷习题)模拟试题(含参考答案).pdf
- 华东理工大学:《信号与系统》课程教学资源(学习指导书)第五章 连续时间系统的复频域分析.pdf
- 华东理工大学:《信号与系统》课程教学资源(学习指导书)第四章 傅里叶变换在系统分析中的应用.pdf
- 华东理工大学:《信号与系统》课程教学资源(学习指导书)第三章 傅里叶变换(连续时间信号的傅里叶分析).pdf
- 华东理工大学:《信号与系统》课程教学资源(学习指导书)第二章 线性时不变系统的时域分析.pdf
- 华东理工大学:《信号与系统》课程教学资源(学习指导书)第一章 信号与系统概述.pdf
- 华东理工大学:《信号与系统》课程教学资源(课件讲稿)第五章 拉普拉斯变换和连续时间系统的复频域分析(2/2).pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第一章 自动控制系统概述.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第二章 过程特性.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第三章 检测变送.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第五章 执行器.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第四章 显示仪表.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第七章 简单控制系统.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第八章 复杂控制系统.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第九章 计算机控制系统.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)第十章 生产过程控制.pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)模拟试卷一(含参考答案).pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(学习指导书)模拟试卷二(含参考答案).pdf
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(参考资料)学术术语关键词.doc
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)总复习.ppt
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)第一章 自动控制系统概述(主讲:叶西宁).ppt
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)第二章 过程特性.ppt
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)第七章 简单控制系统.ppt
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)第三章 过程检测仪表.ppt
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)第五章 执行器.ppt
- 华东理工大学:《测控技术 Measurement and control technology》课程教学资源(PPT课件讲稿)第六章 控制器.ppt
