Coded Caching under Arbitrary Popularity Distributions

Coded Caching under Arbitrary Popularity Distributions Jinbei Zhang,Xiaojun Lin,Xinbing Wang
Coded Caching under Arbitrary Popularity Distributions Jinbei Zhang, Xiaojun Lin, Xinbing Wang

Caching and Coded-Caching Caching is important for reducing backhaul requirement when serving content that many users are interested in The cache size at each user needs to be reasonable large compared to the amount of "popular"content Server Coded caching can further reduce the backhaul requirement even when each individual cache size is small, but the global cache size is substantial [Maddah-Ali and cache cache cache Neisen '14] User 1 User 2 User 3 2
Caching and Coded-Caching 2 Server cache cache cache User 1 User 2 User 3 • Caching is important for reducing backhaul requirement when serving content that many users are interested in • The cache size at each user needs to be reasonable large compared to the amount of “popular” content • Coded caching can further reduce the backhaul requirement even when each individual cache size is small, but the global cache size is substantial [Maddah-Ali and Neisen ’14]
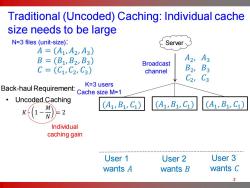
Traditional (Uncoded)Caching:Individual cache size needs to be large N=3 files (unit-size): Server A=(A1,A2A3) B=(B1,B2,B3) A2 A3 Broadcast C=(C1,C2,C3) channel , B3 C2, 3 K=3 users Back-haul Requirement:Cache size M=1 Uncoded Caching (A1,B1C1) (A1,B1C1) (A1,B1C1) Individual caching gain User 1 User 2 User 3 wants A wants B wants C 3
3 (𝐴1 , 𝐵1 , 𝐶1 ) User 1 wants 𝐴 User 2 wants 𝐵 User 3 wants 𝐶 Traditional (Uncoded) Caching: Individual cache size needs to be large Server K=3 users Cache size M=1 Broadcast channel 𝐴 = (𝐴1 , 𝐴2 , 𝐴3 ) 𝐵 = (𝐵1 , 𝐵2 , 𝐵3 ) 𝐶 = (𝐶1 , 𝐶2 , 𝐶3 ) N=3 files (unit-size): • Uncoded Caching 𝐾 ∙ 1 − 𝑀 𝑁 = 2 Back-haul Requirement: (𝐴1 , 𝐵1 , 𝐶1 ) (𝐴1 , 𝐵1 , 𝐶1 ) 𝐴2 , 𝐴3 𝐵2 , 𝐵3 𝐶2 , 𝐶3 Individual caching gain

Coded Caching:Global Caching Gains N=3 files:A=(A1,A2,A3) Server B=(B1,B2B3) C=(C1,C2,C3) Broadcast A2 ⊕ channel B3 中 BG2 K=3 users Back-haul Requirement:Cache size M=1 Uncoded Caching K(1-9)=2 (A1,B1C1) (A2,B2,C2) (A3,B3C3) Bi Coded Caching [1] A3 B3 C2 Global caching User 1 User 2 User 3 gain wants A wants B wants C [1]Fundamental Limits of Caching,M.Maddah-Ali and U.Niesen,IEEE Trans.Inf.Theory,2014. 4
4 (𝐴1 , 𝐵1 , 𝐶1 ) (𝐴2 , 𝐵2 , 𝐶2 ) (𝐴3 , 𝐵3 , 𝐶3 ) 𝐴2 ⊕ 𝐵1 𝐴2 𝐵1 𝐴3 ⊕ 𝐶1 𝐴3 𝐶1 𝐵3 ⊕ 𝐶2 𝐵3 𝐶2 User 1 wants 𝐴 User 2 wants 𝐵 User 3 wants 𝐶 Coded Caching: Global Caching Gains Server 𝐾 ∙ 1 − 𝑀 𝑁 ∙ 1 1 + 𝐾𝑀 𝑁 = 1 • Coded Caching [1] [1] Fundamental Limits of Caching, M. Maddah-Ali and U. Niesen, IEEE Trans. Inf. Theory, 2014. K=3 users Cache size M=1 Broadcast channel 𝐴 = (𝐴1 , 𝐴2 , 𝐴3 ) 𝐵 = (𝐵1 , 𝐵2 , 𝐵3 ) 𝐶 = (𝐶1 , 𝐶2 , 𝐶3 ) N=3 files: Global caching gain • Uncoded Caching 𝐾 ∙ 1 − 𝑀 𝑁 = 2 Back-haul Requirement:

Average-Case vs.Worst-Case NK ·Expected rate: r(Wi)P(Wi) i=1 Worst-case rate [Maddah-Ali and Niesen '14]: max r(Wi) i=1,...NK ·Obviously: NK r(W)P(W)≤ max.r(Wi) i=1,...NK i=1 However,constant-factorresults do NOT carry over from the worst case to the average case max r(Wi) i=1,....NK r(W:)P(W) ≤C maxr*(Wi) ≤c-X→ i=1,...NK Σr*(W)P(W) 5
Average-Case vs. Worst-Case 5 • Expected rate: • Worst-case rate [Maddah-Ali and Niesen `14]: • Obviously: • However, constant-factor results do NOT carry over from the worst case to the average case 𝑖=1 𝑁 𝐾 𝑟(𝑊𝑖)𝑃(𝑊𝑖) max 𝑖=1,…,𝑁𝐾 𝑟(𝑊𝑖 ) 𝑖=1 𝑁 𝐾 𝑟(𝑊𝑖 )𝑃 𝑊𝑖 ≤ max 𝑖=1,…,𝑁𝐾 𝑟(𝑊𝑖 ) max 𝑖=1,…,𝑁𝐾 𝑟(𝑊𝑖) max 𝑖=1,…,𝑁𝐾 𝑟 ∗(𝑊𝑖) ≤ 𝑐 σ𝑖=1 𝑁 𝐾 𝑟(𝑊𝑖)𝑃(𝑊𝑖) σ𝑖=1 𝑁𝐾 𝑟 ∗(𝑊𝑖)𝑃(𝑊𝑖) ≤ 𝑐

Related Work on the Average Case U.Niesen,and M.A.Maddah-Ali,"Coded Caching with Nonuniform Demands", arXiv:1308.0178v2[cs.T,Mar.2014.(TT2016) >Divide the files into groups The gap between the lower bound and the achievable (upper)bound increases with of groups(unbounded) J.Hachem,N.Karamchandani and S.Diggavi,"Multi-level Coded Caching", arXiv.1404.6563[cs.lT],Apr.2014. Popularity has multiple levels The gap increases with of levels (unbounded) e M.Ji,A.Tulino,J.Llorca and G.Caire,"On the Average Performance of Caching and Coded Multicasting with Random Demands",arXiv:1402.4576v2 [cs.1d,Jul.2014. zipfpopularity distribution The gap increases with when a 1(unbounded) 6
Related Work on the Average Case • U. Niesen, and M.A. Maddah-Ali, “Coded Caching with Nonuniform Demands”, arXiv:1308.0178v2 [cs.IT], Mar. 2014. (TIT 2016) ➢ Divide the files into groups ➢ The gap between the lower bound and the achievable (upper) bound increases with # of groups (unbounded) • J. Hachem, N. Karamchandani and S. Diggavi, “Multi-level Coded Caching”, arXiv:1404.6563 [cs.IT], Apr. 2014. ➢ Popularity has multiple levels ➢ The gap increases with # of levels (unbounded) • M. Ji, A. Tulino, J. Llorca and G. Caire, “On the Average Performance of Caching and Coded Multicasting with Random Demands”, arXiv:1402.4576v2 [cs.IT], Jul. 2014. ➢ Zipf popularity distribution 𝑝𝑖 ∝ 1 𝑖 𝛼 ➢ The gap increases with 1 𝛼−1 when 𝛼 > 1 (unbounded) 6

The Open Question Can we find a coded caching scheme whose average-case performance is at most a constant factor away from the minimum independently of any popularity distributions? 7
The Open Question 7 Can we find a coded caching scheme whose average-case performance is at most a constant factor away from the minimum independently of any popularity distributions?

Our Main Results Constant-factor gap between the lower bound(Ru)and the achievable (upper)bound(Rb)of the expected backhual transmission rate: Rub≤87Rb+2→Rub≤55Rb The achievable bound (Rub) is attained by a simple coded Popularity caching scheme similar to [Ji et al '14] Perform coded caching only 1 among the most popular KM N files - However,all N popular files are Ni File treated uniformly Index The key step is to show a matching lower bound Arbitrary Popularity Distribution! 8
Our Main Results • Constant-factor gap between the lower bound (𝑅𝑙𝑏) and the achievable (upper) bound (𝑅𝑢𝑏) of the expected backhual transmission rate: 𝑅𝑢𝑏 ≤ 87𝑅𝑙𝑏 +2 𝑅𝑢𝑏≤ 55𝑅𝑙𝑏 • The achievable bound (𝑅𝑢𝑏 ) is attained by a simple coded caching scheme similar to [Ji et al ’14] – Perform coded caching only among the most popular N1 files – However, all N1 popular files are treated uniformly • The key step is to show a matching lower bound 8 Arbitrary Popularity Distribution! File Index Popularity 1 𝐾𝑀 𝑁1
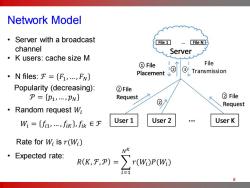
Network Model Server with a broadcast File 1 File N channel Server ·K users:cache size M 人人 ①File File ·N files:F={F,,FN} Transmission Popularity (decreasing): ②File P={p1,,pN} Request ②File 2 Request ·Random request Wi W={fi,,fik},fi欣∈F User 1 User 2 .. User K Rate for Wi is r(Wi) 。Expected rate: R(K,F,P)=>r(Wi)P(W:) i=1 9
Network Model 9 • Server with a broadcast channel • K users: cache size M • N files: ℱ = 𝐹1, …, 𝐹𝑁 • Random request 𝑊𝑖 • Expected rate: Popularity (decreasing): 𝒫 = 𝑝1,… , 𝑝𝑁 𝑊𝑖 = 𝑓𝑖1, … , 𝑓𝑖𝐾 , 𝑓𝑖𝑘 ∈ ℱ Rate for 𝑊𝑖 is 𝑟(𝑊𝑖) 𝑅 𝐾, ℱ,𝒫 = 𝑖=1 𝑁 𝐾 𝑟(𝑊𝑖)𝑃(𝑊𝑖) User 1 File 1 ... File N User 2 ... User K Server File Placement User 1 File 1 ... File N User 2 ... User K 1 Server File Placement User 1 File 1 ... File N User 2 ... User K File Request File Request 1 2 2 2 2 Server File Placement User 1 File 1 ... File N User 2 ... User K File Request File Request File Transmission 1 2 3 2 2 2 Server

Main Intuition:An "Insensitivity"Property ·The“best”worst-case rate Uncoded caching N-M ”71 for serving N files can be Coded achieved by uniform caching N -1 caching [Maddah-Ali and Niesen '14] M 1 K.(1- M) N M KM 1- M M N N K M whenever K >N/M Key Insight:Beyond K=N/M,the above rate is independent of the number of users K Due to its global caching gain,coded caching significantly reduce the threshold for this insensitivity to arise 10
• The “best” worst-case rate for serving N files can be achieved by uniform caching [Maddah-Ali and Niesen ’14] whenever K >> N/M • Key Insight: Beyond K=N/M, the above rate is independent of the number of users K • Due to its global caching gain, coded caching significantly reduce the threshold for this insensitivity to arise 10 Main Intuition: An “Insensitivity” Property K 𝑁 𝑀 − 1 Coded caching 𝑁 Uncoded caching 𝑁 − 𝑀 𝑁 𝑀 1 (1 ) (1 ) 1 1 M N M N K N M N M KM N • − • − = − +
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- Coded Caching under Arbitrary Popularity Distributions.pdf
- On the Similarity between von Neumann Graph Entropy and Structural Information:Interpretation, Computation, and Applications.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第12章 文件.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第8章 动态存储管理.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第9章 查找.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第5章 广义表.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第7章 图.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(教案讲义)第7章 图(图的遍历算法及其应用).doc
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第6章 树和二叉树.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(教案讲义)第6章 树和二叉树.doc
- 中国科学技术大学:《数据结构及其算法》课程教学资源(教案讲义)第4章 串、数组和广义表.doc
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第4章 串.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(教案讲义)第3章 栈和队列.doc
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第3章 栈和队列.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第2章 线性表.pdf
- 中国科学技术大学:《数据结构及其算法》课程教学资源(教案讲义)第2章 线性表.doc
- 中国科学技术大学:《数据结构及其算法》课程教学资源(教案讲义)第1章 绪论(主讲:张昱、马建辉).doc
- 中国科学技术大学:《数据结构及其算法》课程教学资源(课件讲稿)第1章 绪论(主讲:张昱、马建辉).pdf
- 中国科学技术大学:《编译原理与技术》课程教学资源(课件讲稿)第9章 面向对象语言的编译.pdf
- 中国科学技术大学:《编译原理与技术》课程教学资源(课件讲稿)第8章 编译系统和运行系统.pdf
- Distributed Multicast Tree Construction in Wireless Sensor Networks.pdf
- A Distributed Algorithm to Construct Multicast Trees in WSNs:An Approximate Steiner Tree Approach.pptx
- FINE:A Framework for Distributed Learning on Incomplete Observations for Heterogeneous Crowdsensing Networks.pdf
- Joint Optimization of Multicast Energy in Delay-constrained Mobile Wireless Networks.pdf
- Determining Source-Destination Connectivity in Uncertain Networks:Modeling and Solutions.pdf
- Throughput and Delay Scaling of General Cognitive Networks.pdf
- Heterogeneity Increases Multicast Capacity In Clustered Network.ppt
- Mobility Increases the Connectivity of K-hop Clustered Wireless Networks.ppt
- Fundamental Relationship between Node Density and Delay in Wireless Ad Hoc Networks with Unreliable Links.ppt
- MotionCast:On the Capacity and Delay Tradeoffs.ppt
- Optimal Determination of Source-destination Connectivity in Random Graphs.ppt
- Coverage and Energy Consumption Control in Mobile Heterogeneous Wireless Sensor Networks.pdf
- DRIMUX:Dynamic Rumor Influence Minimization with User Experience in Social Networks.pdf
- Achieving 100% Throughput in TCP/AQM Under Aggressive Packet Marking With Small Buffer.pdf
- Delay and Capacity Tradeoff Analysis for MotionCast.pdf
- Multicast Performance With Hierarchical Cooperation.pdf
- Capacity Scaling of General Cognitive Networks.pdf
- Mobility Increases the Connectivity of Wireless Networks.pdf
- Asymptotic Analysis on Secrecy Capacity in Large-Scale Wireless Networks.pdf
- Asymptotic Analysis on Secrecy Capacity in Large-Scale Wireless Networks.ppt
