电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第4章 回归分类

回归分类 电子科技大学 师君
电子科技大学 师 君

最小二乘问题 线性分类 广义线性分类 稀疏重建
最小二乘问题 线性分类 广义线性分类 稀疏重建
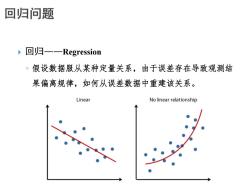
回归问题 ,回归一一Regression 。假设数据服从某种定量关系,由于误差存在导致观测结 果偏离规律,如何从误差数据中重建该关系。 Linear No linear relationship
回归——Regression ◦ 假设数据服从某种定量关系,由于误差存在导致观测结 果偏离规律,如何从误差数据中重建该关系

回归问题 ,最小二乘准则 。回归残差 e;=f(x;w)-y e=leez,ex 。最小二乘准则: w*=argmin∑f(x;w)-y,'=argmin(e'c)
最小二乘准则 ◦ 回归残差 ◦ 最小二乘准则: 2 * argmin ( ; ) argmin T i i i P f x w y w w w e e 1 2 ( ; ) , ,... i i i T N e f y e e e x w e

回归问题 ,线性回归 。狭义线性回归一一 线性函数 f(x;w)=wx 。广义线性回归一一基函数的线性组合 f(x;w)=>w:0:(x)=w"(o(x)) p(x)=((x)(x)..x(x)
线性回归 ◦ 狭义线性回归——线性函数 ◦ 广义线性回归——基函数的线性组合 ( ; ) T f x w w x 1 2 ( ; ) ... T k k k T K f w x w x w φ x φ x x x x

回归问题 ,最小二乘问题的矩阵模型 。矩阵表示 e,=w'(p(x,))-y=(p(x,))w-x e=ΦW-y 9,(x1)p2().px() 0,(2)p2(2)…px(2) Φ 三 (xx)(xx)..(xx)
最小二乘问题的矩阵模型 ◦ 矩阵表示 1 1 2 1 1 1 2 2 2 2 1 2 ... ... ...... ... T T i i i i i K K N N K N e y y w φ x φ x w e w y x x x x x x x x x

回归问题 ,最小二乘问题的矩阵模型 w*arg min e=arg minw-y =argmin(e'e) =argmin[(Φw-y)'(Φw-y)]
最小二乘问题的矩阵模型 2 2 2 2 * arg min arg min arg min arg min T T w w w w w e w y e e w y w y

回归问题 ,最小二乘解 e'e=(④w-y)'(④w-y) =wIΦΦw-2wΦ'y+yy ae'e=2ΦΦw-2Φ'y=0 ∂w →w=(DΦ)'Φ'y MP广义逆矩阵
最小二乘解 1 = 2 2 2 0 T T T T T T T T T T T T e e w y w y w w w y y y e e w y w w y MP广义逆矩阵

最小二乘问题 线性分类 广义线性分类 稀疏重建
最小二乘问题 线性分类 广义线性分类 稀疏重建
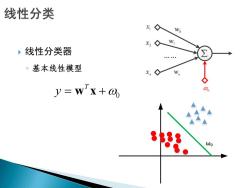
线性分类 W x2 w ,线性分类器 。基本线性模型 x y=Wx+0o 8。 Wo
线性分类器 ◦ 基本线性模型 0 T y w x ω0
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第3章 统计分类.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第2章 数值最优化介绍.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第1章 机器学习介绍(师君).pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)09 CDN内容分发网络.pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)11 社会计算(二).pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)11 社会计算(一).pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)10 物联网.pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)08 域名系统.pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)07 P2P网络(二)Distributed Hash Table.pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)06 P2P网络(一).pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)05 云计算(三)数据一致性理论.pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)04 云计算(二).pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)03 云计算(一).pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)02 网格计算.pdf
- 电子科技大学:《网络计算模式 Network Computing Paradigm》课程教学资源(课件讲稿)01 概述及企业计算(丁熠).pdf
- 电子科技大学:《网络安全理论与技术 Theory and technology of network security》课程教学资源(课件讲稿)第十章 总结与展望.pdf
- 电子科技大学:《网络安全理论与技术 Theory and technology of network security》课程教学资源(课件讲稿)第八章 防火墙与VPN技术.pdf
- 电子科技大学:《网络安全理论与技术 Theory and technology of network security》课程教学资源(课件讲稿)第九章 入侵检测与入侵防御技术.pdf
- 电子科技大学:《网络安全理论与技术 Theory and technology of network security》课程教学资源(课件讲稿)第七章 访问控制.pdf
- 电子科技大学:《网络安全理论与技术 Theory and technology of network security》课程教学资源(课件讲稿)第六章 身份认证.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第5章 支持向量机.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第6章 深度神经网络.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第7章 非监督分类.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第8章 特征提取与降维.pdf
- 电子科技大学:《机器学习 Machine Learning》课程教学资源(课件讲稿)第9章 Markov马尔科夫分类.pdf
- 电子科技大学:《Linux操作系统内核技术 The Linux Kernel Technology》课程教学资源(课件讲稿)第一讲 课程概述(李林).pdf
- 电子科技大学:《Linux操作系统内核技术 The Linux Kernel Technology》课程教学资源(课件讲稿)第二讲 程序员技术手段.pdf
- 电子科技大学:《Linux操作系统内核技术 The Linux Kernel Technology》课程教学资源(课件讲稿)第三讲 指针存储之谜.pdf
- 电子科技大学:《Linux操作系统内核技术 The Linux Kernel Technology》课程教学资源(课件讲稿)第四讲 内核模块不可调试之谜.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 01 面向对象软件开发概述.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 10 Java 高级编程.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 02 Java 概述.ppt
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 03 Java 编程入门.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 03 Java 编程入门.ppt
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 04 Java 语言基础.ppt
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 05 Java 类.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 05 Java 类.ppt
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 06 继承与多态.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 07 Java 工具类.pdf
- 南京大学:《Java语言程序设计 Programming in Java》课程教学资源(教案讲义)Lecture 08 数据结构与算法.ppt
