上海交通大学：SCM供应链管理 Supply Chain Managment》课程教学资料_lecture notes_LP and Excel solver

Tutorial Solving Linear Programming Problem by Excel solver and the Integer programing Brief introduction: 1.Excel Solver can solve linear programming problems with small size. 2.Professional optimization tools,such as,CPLEX solver,LINDO are used to handle LP problem with large size

Brief introduction: 1. Excel Solver can solve linear programming problems with small size. 2. Professional optimization tools, such as, CPLEX solver, LINDO are used to handle LP problem with large size

Outline Excel solver for linear programming o Techniques to formulate problem by using binary variables

Outline Excel solver for linear programming Techniques to formulate problem by using binary variables

Solve LP by Excel solver Example 1: min Z=3x1 2x2 s.t 2x1+x2 ≥ 10 -3x1+2x2 ≤6 C1+C2 ≥6 x1≥0， x2≥0. ● This problem is called linear programming problem,since the objective function and the constraints are linear and the decision variables are continuous. If all the decision variable can only take integer value,then the problem is called the integer programming problem. If some of the decision variables take only the integer value,this problem is called the mixed-integer programming problem

Solve LP by Excel solver Example 1:  This problem is called linear programming problem, since the objective function and the constraints are linear and the decision variables are continuous.  If all the decision variable can only take integer value, then the problem is called the integer programming problem.  If some of the decision variables take only the integer value, this problem is called the mixed-integer programming problem

Solve LP by Excel solver(continue) -Represent the decision variables by the cells in ECXEL.In our example, “$A$1”and“$A$2”are used to represent the decision variable x1 and x2 respectively.Fill the initial value of them (e.g."O"). Select a cell to represent objective function.In the example,"SA$3" represents objective function and it is filled by formula"=3*$A$1+2*$A$2". -Select cells to represent constraints.For example,"$B$1"represents the left-hand-side of constraint 1 and it is filled by formula “=2*$A$1+$A$2”.The cell“$C$1”represents the right-hand-side of constraint1 and it is filled by“6”.Similarly,“$B$2”and“$B$3”represents the left-hand-side of constraints2and3.“$C$2”and“$C$3”represents the right-hand-side of constraints 2 and 3

Solve LP by Excel solver (continue)  Represent the decision variables by the cells in ECXEL . In our example, “$A$1” and “$A$2” are used to represent the decision variable x1 and x2 respectively. Fill the initial value of them (e.g. “0”).  Select a cell to represent objective function. In the example, “$A$3” represents objective function and it is filled by formula “=3*$A$1+2*$A$2”.  Select cells to represent constraints. For example, “$B$1” represents the left-hand-side of constraint 1 and it is filled by formula “=2*$A$1+$A$2”. The cell “$C$1” represents the right-hand-side of constraint 1 and it is filled by “6”. Similarly, “$B$2” and “$B$3” represents the left-hand-side of constraints 2 and 3. “$C$2” and “$C$3” represents the right-hand-side of constraints 2 and 3

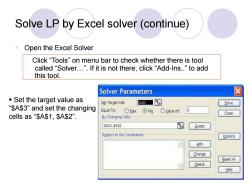
Solve LP by Excel solver (continue) Open the Excel Solver Click "Tools"on menu bar to check whether there is tool called“Solver..”.If it is not there,click“Add-lns.”to add this tool. Solver Parameters Set the target value as Set Target Cell: 5As3 国 Solve “$A$3”and set the changing Equal To: Max OM恤 OValue of: 0 Close cells as“$A$1,$A$2”. By Changing Cells: SA$1,$A52 Guess Subject to the Constraints: Options Add Change Reset All Delete Help

Solve LP by Excel solver (continue)  Open the Excel Solver Click “Tools” on menu bar to check whether there is tool called “Solver…”. If it is not there, click “Add-Ins..” to add this tool.  Set the target value as “$A$3” and set the changing cells as “$A$1, $A$2

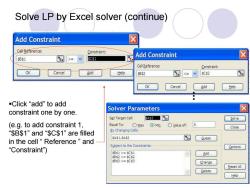
Solve LP by Excel solver (continue) Add Constraint ☒ Cell-Reference: Constraint: Add Constraint 国 ☒ B51 >=V Cell Reference: Constraint: OK Cancel Add Help $892 $0s2 OK Cancel Add Help Click“add”to add Solver Parameters constraint one by one. Set Target Cell: SAS3 国 Solve (e.g.to add constraint 1, Equal To: Max Min OYalue of: 0 Close “$B$1”and“$C$1”are filled By Changing Cells: SAS1,SAS2 Guess in the cell“Reference”and Subject to the Constraints: “Constraint Options SBs1>=$C$1 Add $852=$Cs3 Change Reset All Delete Help

Solve LP by Excel solver (continue) Click “add” to add constraint one by one. (e.g. to add constraint 1, “$B$1” and “$C$1” are filled in the cell “ Reference ” and “Constraint”)

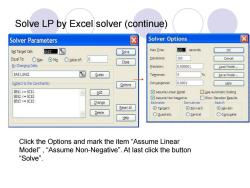
Solve LP by Excel solver (continue) Solver Parameters Solver Options ☒ Set Target Cell: SAS3 Solve Max Iime: 100 seconds OK Equal To: OMax OM血 OValue of: 0 Iterations: 100 Cancel Close By Changing Cells: Precision: 0.000001 Load Model... SAS1,SAS2 Guess Tolerance: 5 % Save Model... Subject to the Constraints: Options Conyergence: 0.0001 Help s851>=5051 Add ☑Assume Linear Model ▣Use Automatic Scaling S8$2=$C$3 Change Estimates Derivatives Search Reset All OTangent Eorward Newton Delete ○Quadratic ○Central ○Conjugate Help Click the Options and mark the item"Assume Linear Model'"”,“Assume Non-Negative”.At last click the button “Sove

Solve LP by Excel solver (continue) Click the Options and mark the item “Assume Linear Model” , “Assume Non-Negative”. At last click the button “Solve

Solve LP by Excel solver (continue) Microsoft Excel-Book1 File Edit View Insert Format Io : 3县3|昌g单」名里 C1 10 A B C D 1 4 10 10 2 2 -8 6 3 16 6 6 4 The Optimal solution is (x1,x2)=(4,2)and the optimal value is 16

Solve LP by Excel solver (continue) The Optimal solution is (x1 ,x2 )=(4,2) and the optimal value is 16

Exercise Example 2:Solve this problem by EXCEL solver (P1) Maximize Z=51+522+8x3-2x4-4x5 Subject to -321+6x2-7x3+9x4+9x5 10 x1+2x2-x4-3x5≤0 x1≤1， x2≤1， x3≤1， x4≤1， x5≤1， xj≥0f0rj=1,2,.5

Exercise Example 2: Solve this problem by EXCEL solver

Outline Excel solver for linear programming o Techniques to formulate problem by using binary variables

Outline Excel solver for linear programming Techniques to formulate problem by using binary variables