安徽理工大学：《算法设计与分析 Algorithm Design and Analysis》课程教学资源（PPT课件讲稿）第7章 回溯法

第8章回溯法

第8章 回溯法

回溯法概述 。回溯法可以系统的搜索一个问题的所有解或任一 个解 ·它在包含问题的所有解的解空间树中，按照深度 优先的策略，从根结点出发搜索解空间树。算法 搜索到某一结点时，如果断定该结点肯定不包含 问题的解，则跳过以该结点为根的子树的搜索， 逐层向其祖先结点回溯 ·这种以深度优先方式搜索问题的解的方法称为回 溯法

回溯法概述 回溯法可以系统的搜索一个问题的所有解或任一 个解 它在包含问题的所有解的解空间树中，按照深度 优先的策略，从根结点出发搜索解空间树。算法 搜索到某一结点时，如果断定该结点肯定不包含 问题的解，则跳过以该结点为根的子树的搜索， 逐层向其祖先结点回溯 这种以深度优先方式搜索问题的解的方法称为回 溯法

可用▣溯法求解的问题 O 问题的解可以用一个n元组(x1,…,x)来表示， 其中的x取自于某个有穷集S,并且这些解 必须使得某一规范函数P(x,.,X)（也称限 界函数)取极值或满足该规范函数条件。 0例子：A(1:n)个元素的分类问题 问题的解为n元组： x取自有穷集； 规范函数P:A(X)=A(X+)

可用回溯法求解的问题 问题的解可以用一个n元组(x1 ,…,xn )来表示， 其中的xi取自于某个有穷集Si，并且这些解 必须使得某一规范函数P(x1 ,…,xn )（也称限 界函数）取极值或满足该规范函数条件。 例子：A(1:n)个元素的分类问题 ◼ 问题的解为n元组； ◼ xi取自有穷集； ◼ 规范函数P：A(xi )<=A(xi+1)

问题求解的方法 ·便性处理法 列出所有候选解，逐个检查是否为所需要的解 理论上，候选解数量有限，并且通过检查所有或部分候 选解能够得到所需解时，上述方法可行 实际中则很少使用，因为候选解的数量通常都非常大 (比如指数级，甚至是大数阶乘)，即便采用最快的计 算机也只能解决规模较小的问题。 回溯或分枝限界法 避免对很大的候选解集合进行完全检查 大大减少问题的求解时间 通常用来求解规模较大的问题

问题求解的方法 硬性处理法 ◼ 列出所有候选解，逐个检查是否为所需要的解 ◼ 理论上，候选解数量有限，并且通过检查所有或部分候 选解能够得到所需解时，上述方法可行 ◼ 实际中则很少使用，因为候选解的数量通常都非常大 （比如指数级，甚至是大数阶乘），即便采用最快的计 算机也只能解决规模较小的问题。 回溯或分枝限界法 ◼ 避免对很大的候选解集合进行完全检查 ◼ 大大减少问题的求解时间 ◼ 通常用来求解规模较大的问题

回溯法思想 第一步：为问题定义一个状态空间(state space), 这个空间必须至少包含问题的一个解 著雨羞男緹整窗姜朝以便它能被谷易地搜素。真 第三步：按深度优先的方法从开始结点进行搜索 开始结点是一个活结点（也是E-结点：expansion node) 如果能从当前的E-结点移动到一个新结点，那么这个新 结点将变成一个活结点和新的E结点，旧的E结点仍是 一个活结点。 如果不能移到一个新结点，当前的E-结点就“死”了 C 即不再是一个活结点)，那么便只能返回到最近被考 察的活结点（回溯)，这个活结点变成了新的结点。 聚程篝 我们已经找到了答案或者回溯尽了所有的活结点时

回溯法思想 第一步：为问题定义一个状态空间(state space)， 这个空间必须至少包含问题的一个解 第二步：组织状态空间以便它能被容易地搜索。典 型的组织方法是图或树 第三步：按深度优先的方法从开始结点进行搜索 ◼ 开始结点是一个活结点（也是 E-结点：expansion node） ◼ 如果能从当前的E-结点移动到一个新结点，那么这个新 结点将变成一个活结点和新的E-结点，旧的E-结点仍是 一个活结点。 ◼ 如果不能移到一个新结点，当前的E-结点就“死”了 （即不再是一个活结点），那么便只能返回到最近被考 察的活结点（回溯），这个活结点变成了新的E-结点。 ◼ 当我们已经找到了答案或者回溯尽了所有的活结点时， 搜索过程结束

回溯法如何提高效率？ ●由开始结点到当前E-结点构成解向量 (X1.,X) ·如果判定(x1,x)不能导致最优解，那么就 将可能要测试的m+1.mn个向量略去。 ©因此回溯法的测试次数比硬性处理作的测 试次数要少得多。 如何判定（区1）能否导致最优解？

回溯法如何提高效率？ 由开始结点到当前E-结点构成解向量 (x1 ,…,xi ) 如果判定(x1 ,…,xi )不能导致最优解，那么就 将可能要测试的mi+1…mn个向量略去。 因此回溯法的测试次数比硬性处理作的测 试次数要少得多。 ◼ 如何判定(x1 ,…,xi )能否导致最优解？

约束条件 回溯法的解需要满足一组综合的约束条件， 通常分为：显式约束和隐式约束 e、 显式约束条件限定每个x只从一个给定的集 合上取值，例如： X分=0 即s=所有非负实数} X=0或x=1 即s={0,1} =X<=u 即s={a:l<=a<=u e 满足显式约束的所有元组确定一个可能的解 空间 ©隐式约束描述了x必须彼此相关的情沉，如 0/1背包问题中的背包重量M

约束条件 回溯法的解需要满足一组综合的约束条件， 通常分为：显式约束和隐式约束 显式约束条件限定每个xi只从一个给定的集 合上取值，例如： ◼ xi>=0 即si={所有非负实数} ◼ xi=0或xi=1 即 si={0,1} ◼ l<=xi<=u 即si={a:l<=a<=u} 满足显式约束的所有元组确定一个可能的解 空间 隐式约束描述了xi必须彼此相关的情况，如 0/1背包问题中的背包重量M

回溯法求解的经典问题(1) 8-皇后问题 。在一个8*8棋盘上放置8个皇后，且使得每两 个之间都不能互相“攻击”，也就是使得每 两个都不能在同一行、同一列及同一条斜角 线上。 ®8皇后问题的解可以表示为8-元组(X1,.,X)， 其中其中x:是第i行皇后所在的列号， 。 0显式约束条件是x={1,2,3,4,5,6,7,8},1≤1≤8 。隐式约束条件是，没有两个x可以相同且没 有两个皇后可以在同一条斜角线上

回溯法求解的经典问题（1） 8-皇后问题 在一个8*8棋盘上放置8个皇后，且使得每两 个之间都不能互相“攻击”，也就是使得每 两个都不能在同一行、同一列及同一条斜角 线上。 8皇后问题的解可以表示为8-元组(x1 ,…,x8 ) ， 其中其中xi是第i行皇后所在的列号。 显式约束条件是xi={1,2,3,4,5,6,7,8}, 1≤i≤8 隐式约束条件是，没有两个xi可以相同且没 有两个皇后可以在同一条斜角线上

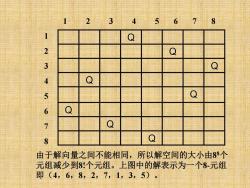
12345678 1 Q 234 Q Q Q 567 Q 8 Q 由于解向量之间不能相同，所以解空间的大小由88个 元组减少到8：个元组。上图中的解表示为一个8-元组 即(4,6,8,2,7,1,3,5)

Q Q Q Q Q Q Q Q 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 由于解向量之间不能相同，所以解空间的大小由8 8个 元组减少到8!个元组。上图中的解表示为一个8-元组 即（4，6，8，2，7，1，3，5）

回溯法求解的经典问题（2) 子集和数问题 已知(w1,W2,.,wn)和M,均为正数。要求找出w的和数等 于M的所有子集。 例如：若n=4,(w1,w2,W3,w4)=(11,13,24,7),M=31,则满足要 求的子集是(11,13,7)和(24,7). 子集和数问题解的一种表示方法 0若用W的下标表示解向量，这两个解向量为(1,2,4)和 (3,4)。 子集和数问题的解可以表示为k-元组(x1,x2,,xx),1≤k≤n 并且不同的解可以是大小不同的元组。 显式约束条件是x∈为整数且1jn。 隐式约束条件是 1)没有两个x是相同的； 2)wx的和为M; 3)x≤x+1,1≤i<n(避免产生同一个子集的重复情况)

回溯法求解的经典问题（2） 子集和数问题 已知(w1 , w2 , …, wn )和M，均为正数。要求找出wi的和数等 于M的所有子集。 例如：若n=4,(w1,w2,w3,w4)=(11,13,24,7),M=31，则满足要 求的子集是(11,13,7)和(24,7). 子集和数问题解的一种表示方法 若用Wi的下标表示解向量，这两个解向量为(1,2,4)和 (3,4)。 子集和数问题的解可以表示为k-元组(x1 , x2 , …, xk ), 1≤k≤n 并且不同的解可以是大小不同的元组。 显式约束条件是xi∈{j|j为整数且1≤j≤n}。 隐式约束条件是 ◼ 1)没有两个xi是相同的; ◼ 2)wxi的和为M; ◼ 3)xi＜xi＋1 ,1≤i＜n（避免产生同一个子集的重复情况）