海南大学：《生物统计学》课程教学资源（试卷习题）生统试题库7（含参考答案）

生物统计学试题库 七 一、解释以下术语及符号20分 样本： 试验指标： 交互效应： 局部控制： 对照： 准确度： S2: ta: F处理： p: 二、填空题20分 1、统计分析的核心在于由 的情况推断的信息。 2、试验设计要贯彻 等三大原则。 3、反映资料中心位置的统计量有 ；反映样本大小的统计量 有： ；反映数据变异度的统计量常用的有 等。 4、当用样本统计量去对相应的总体参数进行估计时，如果该样本统计量比总体 参数 和 的机会相等，则称这样的估计为

1 生物统计学试题库 七 一、解释以下术语及符号 20 分 样本： 试验指标： 交互效应： 局部控制： 对照： 准确度： S 2 ： tα ： F 处理 ： ρ： 二、填空题 20 分 1、统计分析的核心在于由 的情况推断 的信息。 2、试验设计要贯彻 、 、 等三大原则。 3、反映资料中心位置的统计量有 ；反映样本大小的统计量 有： ； ；反映数据变异度的统计量常用的有_ _、 _ _、 等。 4、当用样本统计量去对相应的总体参数进行估计时，如果该样本统计量比总体 参数 和 的机会相等，则称这样的估计为

5、试验资料一定要满足 等三条件才能 进行方差分析。若试验资料为可数资料，在进行方差分析时，常用的统计代换 有 等三种。 三、简答题10分 1、请说明试验设计三原则各自的内容与作用。 2、请分别解释统计假设μ=μ品.·=μ成立与不成立的统计意义。 四、问答题10分 现有4个品种需要在一坡地上进行产量比较，请设计一适合的试验方案（要求 写清楚设计步骤并画图) 五、计算题40分 1、对甘蔗含糖量测定得数据：8,8,9,9,9,10,10,10,11,12（单位：%）， 计算此资料的平均数、自由度、平方和、标准差、标准误，并求其置信度为95% 的区间。ta.05=2.306;t0.s=2.262;to.s,o=2.228; 2、现对施药区30个果实进行测定得平均重量为32g,平方和为560；对照区30 个果实的平均重量为29g,平方和为710，试分析施药对提高果实重量有无效果。 to.0s-2.00;to.o1=2.66 3、现对4种肥料施进行比较试验，重复5次测定产量数据，试完成下表中的F 测验并写出结论

2 5、 试验资料一定要满足_ _、_ _、_ _等三条件才能 进行方差分析。若试验资料为可数资料，在进行方差分析时，常用的统计代换 有_ _、_ _、_ _等三种。 三、简答题 10 分 1、请说明试验设计三原则各自的内容与作用。 2、请分别解释统计假设 μA =μB=.=μM 成立与不成立的统计意义。 四、问答题 10 分 现有 4 个品种需要在一坡地上进行产量比较，请设计一适合的试验方案（要求 写清楚设计步骤并画图） 五、计算题 40 分 1、对甘蔗含糖量测定得数据：8, 8, 9, 9, 9, 10, 10, 10, 11, 12 (单位：%)， 计算此资料的平均数、自由度、平方和、标准差、标准误，并求其置信度为 95% 的区间。t0.05,8=2.306; t0 .05,9=2.262; t0 .05,10=2.228; 2、现对施药区 30 个果实进行测定得平均重量为 32g，平方和为 560；对照区 30 个果实的平均重量为 29g，平方和为 710，试分析施药对提高果实重量有无效果。 t0 .05=2.00；t0.01=2.66 3、现对 4 种肥料施进行比较试验，重复 5 次测定产量数据，试完成下表中的 F 测验并写出结论

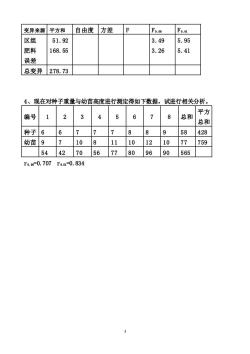
变异来源平方和自由度方差℉ Fo.05 Fo.01 区组 51.92 3.49 5.95 肥料 168.55 3.26 5.41 误差 总变异278.73 4、现在对种子重量与幼苗高度进行测定得如下数据，试进行相关分析。 平方 编号1 2 3 4 6 7 8总和 总和 种子6 6 7 7 7 8 18 958428 幼苗97 1081110121077759 5442705677809690565 r0.5=0.707r0.01=0.834

3 变异来源 平方和 自由度 方差 F F0 .05 F0 .01 区组 肥料 误差 51.92 168.55 3.49 3.26 5.95 5.41 总变异 278.73 4、现在对种子重量与幼苗高度进行测定得如下数据，试进行相关分析。 编号 1 2 3 4 5 6 7 8 总和 平方 总和 种子 6 6 7 7 7 8 8 9 58 428 幼苗 9 7 10 8 11 10 12 10 77 759 54 42 70 56 77 80 96 90 565 r0 .05=0.707 r0.01=0.834

参考答案 一、解释以下术语及符号20分 样本：按一定方法从集团中抽取出来的、用以代表集团的一部分个体所组成的 小群体 试验指标：用以反映试验效果的指示性状一一即试验对象需要被观测和测量的 特征（或属性） 交互效应：不同因子间的想到影响所造成的试验指标在数值上的变异一一即在 一个因子的不同水平下，另一个因子不同水平之间试验指标的差异的差异(2 个因子间的交互作用) 局部控制：当试验空间的环境条件存在趋势性变异时，控制局部范围内（即重 复区内)的环境条件保持一致的作法 对照：用作衡量其他处理优劣标准的处理 准确度：实际观测值与真实值间的符合程度 S2:样本标准差、=SS/df、是离均差的平方和平均数，固可反应个 体间平均差异的平方 t。：显著水准为a的t分布的临界值 F处建：处理间的F值、=S处/S避、是处理间平均差异的平方除 以平均误差的平方，即处理间的差异与误差的比值，可反映差异显著 性的大小 P:集团相关系数，可以反映集团中不同变量之间的相关程度的大小

4 参考答案 一、解释以下术语及符号 20 分 样本：按一定方法从集团中抽取出来的、用以代表集团的一部分个体所组成的 小群体 试验指标：用以反映试验效果的指示性状－－即试验对象需要被观测和测量的 特征（或属性） 交互效应：不同因子间的想到影响所造成的试验指标在数值上的变异－－即在 一个因子的不同水平下，另一个因子不同水平之间试验指标的差异的差异（2 个因子间的交互作用） 局部控制：当试验空间的环境条件存在趋势性变异时，控制局部范围内（即重 复区内）的环境条件保持一致的作法 对照：用作衡量其他处理优劣标准的处理 准确度：实际观测值与真实值间的符合程度 S 2 ：样本标准差、＝SS/df 、是离均差的平方和平均数，固可反应个 体间平均差异的平方 tα ：显著水准为α的 t 分布的临界值 F 处理 ：处理间的 F 值、＝S 2 处理/S2 误差 、是处理间平均差异的平方除 以平均误差的平方，即处理间的差异与误差的比值，可反映差异显著 性的大小 ρ：集团相关系数，可以反映集团中不同变量之间的相关程度的大小

二、填空题20分 1、统计分析的核心在于由样本的情况推断集团的信息。 2、试验设计要贯彻重复、局部控制、随机排列等三大原则。 3、反映资料中心位置的统计量有平均数；反映样本大小的统计量有：样本 容量；自由度；反映数据变异度的统计量常用的有平方和、方差、标 准差（变异系数、级差、标准误一一答对6个中任意3个）等。 6、当用样本统计量去对相应的总体参数进行估计时，如果该样本统计量比总体 参数偏大和偏小的机会相等，则称这样的估计为无偏估计。 7、试验资料一定要满足正态性、同质性、可加性等三条件才能进行方 差分析。若试验资料为可数资料，在进行方差分析时，常用的统计代换有反正 弦代换、平方根代换、对数代换等三种。 三、简答题10分 1、请说明试验设计三原则各自的内容与作用。 重复：每个处理在试验结束后能获得2个及以上的观测值；估计偶然误差；减 小偶然误差 局部控制：当试验空间的环境条件存在趋势性变异时，控制局部范围内（即重 复区内)的环境条件保持一致的作法；减小系统误差（避免系统误差） 随机排列：各处理在小区中的位置由机会决定，并保证每个处理被安排在每个 小区的机会均相等的排列方式：正确估计偶然误差 2、请分别解释统计假设μ=μ三，=μ成立与不成立的统计意义。 此假设成立即指任意两个处理间的差异均不显著（也可说成是相等）；此假设 不成立意指至少其中的某2个处理间存在显著差异（也可说成是有差异或存在 差异)

5 二、填空题 20 分 1、统计分析的核心在于由 样本 的情况推断 集团 的信息。 2、试验设计要贯彻 重复 、 局部控制 、 随机排列 等三大原则。 3、反映资料中心位置的统计量有 平均数 ；反映样本大小的统计量有： 样本 容量 ； 自由度 ；反映数据变异度的统计量常用的有_平方和_、_方差_、 标 准差（变异系数、级差、标准误－－答对 6 个中任意 3 个） 等。 6、当用样本统计量去对相应的总体参数进行估计时，如果该样本统计量比总体 参数 偏大 和 偏小 的机会相等，则称这样的估计为 无偏估计 。 7、 试验资料一定要满足_正态性_、_同质性_、_可加性_等三条件才能进行方 差分析。若试验资料为可数资料，在进行方差分析时，常用的统计代换有_反正 弦代换_、_平方根代换_、_对数代换_等三种。 三、 简答题 10 分 1、请说明试验设计三原则各自的内容与作用。 重复：每个处理在试验结束后能获得 2 个及以上的观测值；估计偶然误差；减 小偶然误差 局部控制：当试验空间的环境条件存在趋势性变异时，控制局部范围内（即重 复区内）的环境条件保持一致的作法；减小系统误差（避免系统误差） 随机排列：各处理在小区中的位置由机会决定，并保证每个处理被安排在每个 小区的机会均相等的排列方式；正确估计偶然误差 2、请分别解释统计假设 μA =μB=.=μM 成立与不成立的统计意义。 此假设成立即指任意两个处理间的差异均不显著（也可说成是相等）；此假设 不成立意指至少其中的某 2 个处理间存在显著差异（也可说成是有差异或存在 差异）

四、问答题10分 现有4个品种需要在一坡地上进行产量比较，请设计一适合的试验方案（要求 写清楚设计步骤并画图) 一、确定重复次数（最少，最多）：因本试验的空间环境条件存在坡度上的变 化，应采用随机区组设计最为合适，如按误差自由度不小于12的标准，则试验 的最少重复次数为n>=(12/(4-1)+1=5 二、按局部控制的要求划分重复区和小区：因试验空间的环境变异方向为坡度 的方向，固应按垂直于坡度的方向进行重复区的划分，然后再按平行于坡度的 方向将每个重复区划分为4个小区，以保证同一重复区内的不同小区间环境条 件能保持最大程度上的一致性 三、将4个品种安排到已经划分好的小区中：把4个品种在每个重复区中通过 抽签进行安排，以贯彻随机排列的原则，并保证每个处理在每个重复区中都能 占有1个小区且仅占1个小区 B A D D B 4 A D A 6 D N C A B V 五、计算题40分 1、对甘蔗含糖量测定得数据：8,8,9,9,9,10,10,10,11,12（单位：%）， 计算此资料的平均数、自由度、平方和、标准差、标准误，并求其置信度为95% 的区间。t.6g=2.306；t0.6.=2.262;to.6.0=2.228: 答 8 8999101010111296 6

6 四、问答题 10 分 现有 4 个品种需要在一坡地上进行产量比较，请设计一适合的试验方案（要求 写清楚设计步骤并画图） 一、确定重复次数（最少，最多）：因本试验的空间环境条件存在坡度上的变 化，应采用随机区组设计最为合适，如按误差自由度不小于 12 的标准，则试验 的最少重复次数为 n>= (12/(4-1))+1=5 二、按局部控制的要求划分重复区和小区：因试验空间的环境变异方向为坡度 的方向，固应按垂直于坡度的方向进行重复区的划分，然后再按平行于坡度的 方向将每个重复区划分为 4 个小区，以保证同一重复区内的不同小区间环境条 件能保持最大程度上的一致性 三、将 4 个品种安排到已经划分好的小区中：把 4 个品种在每个重复区中通过 抽签进行安排，以贯彻随机排列的原则，并保证每个处理在每个重复区中都能 占有 1 个小区且仅占 1 个小区 B C A D C D B A A D B C A B D C C A D B 五、计算题 40 分 1、对甘蔗含糖量测定得数据：8, 8, 9, 9, 9, 10, 10, 10, 11, 12 (单位：%)， 计算此资料的平均数、自由度、平方和、标准差、标准误，并求其置信度为 95% 的区间。t0.05,8=2.306; t0 .05,9=2.262; t0 .05,10=2.228; 答： 8 8 9 9 9 10 10 10 11 12 96 坡 向 I II III IV V

6464818181100100100121144936 平均数=96/10-9.6 自由度=10-1=9 平方和=936-96*96/10=14.4 标准差=sqrt(14.4/9)=1.2649 标准误=1.2649/sqrt(10)=0.4 置信区间9.6士2.262*0.4[8.7,10.5] 2、现对施药区30个果实进行测定得平均重量为32g,平方和为560：对照区30 个果实的平均重量为29g,平方和为710，试分析施药对提高果实重量有无效果。 t0.=2.00;ta.1=2.66 答： 一、假设“1=μ2即施药与不施药2种情况下果实的重量无显著差异 二、计算 t=(32-29)/sqrt(560+710)/(30-1+30-1)*(1/30+1/30) =2.483 三、推断t。.s=2.00〈2.483〈to.m=2.66推翻无效假设，推断差异达显著但 未达极显著，即施药对提高果实重量有显著效果。 3、现对4种肥料施进行比较试验，重复5次测定产量数据，试完成下表中的F 测验并写出结论。 变异来源平方和自由度方差℉ Fo.o5 Fo.o1 区组 51.923 12.982.67 3.49 5.95 肥料 168.55 56.18 11.57 3.26 5.41 误差 58.2612 4.86 总变异278.7319 结论：区组间差异不显著，处理（肥料）间差异达极显著 >

7 64 64 81 81 81 100 100 100 121 144 936 平均数＝96/10=9.6 自由度＝10-1＝9 平方和＝936-96*96/10＝14.4 标准差＝sqrt(14.4/9)＝1.2649 标准误＝1.2649/sqrt(10)＝0.4 置信区间 9.6±2.262*0.4 [8.7, 10.5] 2、现对施药区 30 个果实进行测定得平均重量为 32g，平方和为 560；对照区 30 个果实的平均重量为 29g，平方和为 710，试分析施药对提高果实重量有无效果。 t0 .05=2.00；t0.01=2.66 答： 一、假设 μ1＝μ2 即施药与不施药 2 种情况下果实的重量无显著差异 二、计算 t=(32-29)/sqrt((560+710)/(30-1+30-1)*(1/30+1/30)) = 2.483 三、推断 t0.05=2.00 < 2.483 < t0.01=2.66 推翻无效假设，推断差异达显著但 未达极显著，即施药对提高果实重量有显著效果。 3、现对 4 种肥料施进行比较试验，重复 5 次测定产量数据，试完成下表中的 F 测验并写出结论。 变异来源 平方和 自由度 方差 F F0 .05 F0 .01 区组 肥料 误差 51.92 168.55 58.26 3 4 12 12.98 56.18 4.86 2.67 11.57** 3.49 3.26 5.95 5.41 总变异 278.73 19 结论：区组间差异不显著，处理（肥料）间差异达极显著

4、现在对种子重量与幼苗高度进行测定得如下数据，试进行相关分析。 编号 平方 1 % 4 5 6 1 8总和 总和 种子66 777 88958428 幼苗9 7 108 1110121077 759 5442705677809690565 r0.6=0.707ra.01=0.834 答： 一、假设：p=0 二、计算 r SP/sqrt (SSx SSy) =(565-58*77/8)/sqrt(428-58*58/8)*(75977*77/8) =0.583 三、推断0.583〈r。.s0.707接受无效假设，推断相关关系未达显著

8 4、现在对种子重量与幼苗高度进行测定得如下数据，试进行相关分析。 编号 1 2 3 4 5 6 7 8 总和 平方 总和 种子 6 6 7 7 7 8 8 9 58 428 幼苗 9 7 10 8 11 10 12 10 77 759 54 42 70 56 77 80 96 90 565 r0 .05=0.707 r0.01=0.834 答： 一、假设：ρ＝0 二、计算 r = SP/sqrt(SSx * SSy) = (565-58*77/8)/sqrt((428-58*58/8)*(759-77*77/8)) = 0.583 三、推断 0.583 < r0.05=0.707 接受无效假设，推断相关关系未达显著