华东师范大学：《高等数值分析（高性能计算/并行计算）》课程教学资源（讲义）10 二维Poisson方程的并行求解算法（基于MPI）

華束师免天学|数学科学学院 School of Mathematical Sciences.East China Normal University 二维Poisson方程的 并行求解算法 (基于MPI) http://math.ecnu.edu.cn/~jypan

http://math.ecnu.edu.cn/~jypan 1 二维 Poisson 方程的 并行求解算法 （基于MPI）

华东师范大学数学科学学院 目录页 School of Mathematical Sciences,ECNU Contents 问题的离散 2 Jacobi算法及并行实现 3 基于红黑排序的并行GS算法 http://math.ecnu.edu.cn/~jypan

http://math.ecnu.edu.cn/~jypan 目录页 Contents 华东师范大学 数学科学学院 School of Mathematical Sciences, ECNU http://math.ecnu.edu.cn/~jypan 1 2 问题的离散 Jacobi 算法及并行实现 3 基于红黑排序的并行 GS 算法

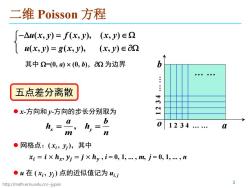
二维Poisson方程 -△u(x,y)=f(x,y) (x,y)∈2 (x,y)=g(x,y), (x,y)∈O2 其中2=(0，)×(0，b),2为边界 b 五点差分离散 ●x-方向和y-方向的步长分别取为 h=a, 1234 L n ●网格点：（x,),其中 xi=i×hx,yj=j×hy,i=0,1,…,m,j=0,1,…,n ●W在(，y)点的近似值记为 http://math.ecnu.edu.cn/~jypan 3

http://math.ecnu.edu.cn/~jypan 3 二维 Poisson 方程 ( , ) ( , ), ( , ) ( , ) ( , ), ( , ) uxy f xy xy uxy gxy xy −∆ = ∈ Ω   = ∈ ∂Ω 其中 Ω=(0, a) × (0, b)，∂Ω 为边界 o a b … … 1 2 3 4 … … 1 2 3 4 … …  x-方向和 y-方向的步长分别取为 , x y a b h h m n = =  网格点：( xi , yj )，其中 𝒙𝒙𝒊𝒊 = 𝒊𝒊 × 𝒉𝒉𝒙𝒙, 𝒚𝒚𝒋𝒋 = 𝒋𝒋 × 𝒉𝒉𝒚𝒚 , i = 0, 1, ... , m, j = 0, 1, ... , n  u 在 ( xi , yj ) 点的近似值记为 ui, j 五点差分离散

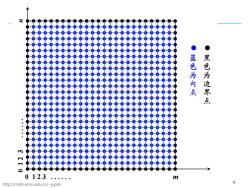
● ● 蓝色为内点 黑色为边界点 0123 m http://math.ecnu.edu.cn/~jypan 4

http://math.ecnu.edu.cn/~jypan 4 0 1 2 3 . . . . . . m 0 1 2 3 . . . . . . n  蓝色为内点  黑色为边界点

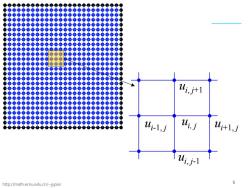
Ui,j计1 Ui-1,j Wi,j 认t1,j Ui,j- http://math.ecnu.edu.cn/~jypan 5

http://math.ecnu.edu.cn/~jypan 5 ui, j ui, j-1 ui+1, j ui, j+1 ui-1, j

二 维Poisson)方程 ■离散后的差分方程为 Ui-\,j u+1,j 24,-4y- 24与-4-4L=j Ui,j-\ h ●边界条件： i=1,.,m-1,j=1,…,n-1 L0=80’m=8in’%oj=80j)Mm=8m fi=f(xi,y),gi=g(xy;) ●整理后可得 4y-d(4+y+4-）-d,(4l+4-i）=lf d 其中 http://math.ecnu.edu.cn/~jypan 6

http://math.ecnu.edu.cn/~jypan 6 二维Poisson方程  离散后的差分方程为 1, 1, , 1 , 1 2 2 2 2 ij i j i j ij i j i j ij x y uu u uu u f h h −− −− + − + − + =  整理后可得 ui,j ui, j-1 ui+1, j ui, j+1 ui-1, j i = 1, ... , m-1, j = 1, ... , n-1 1, 1, , 1 , 1 ( )( ) u d u u d u u df ij x i j i j y i j i j − +− += +− +− ij   边界条件： 0 0 0 0 , , , u gu gu g u g i i in in j j mj mj = = = = ( , ), g ( , ) ij i j ij i j f f x y gx y = = 其中 2 2 22 2 2 , , 2( ) x y x y xy x y h h d d d dd hh h h = = = +

Jacobi迭代 ■求解该差分方程组的Jacobi迭代格式为 4g+w=d小-f+d,(4,+4)+d,(+4) i=1,…,-1,j=1,…,-1 k=0,1,2,… http://math.ecnu.edu.cn/~jypan 7

http://math.ecnu.edu.cn/~jypan 7 Jacobi 迭代  求解该差分方程组的 Jacobi 迭代格式为 ( 1) () () () () 1, 1, , 1 , 1 ( )( ) k kk kk u df d u u d u u ij ij x i j i j y i j i j + =+ + + + +− +−  i = 1, ... , n-1, j = 1, ... , m-1 k = 0, 1, 2,

程序示例 例：取 fx,少=l,gx,八=-2+y2 4 此时Poisson方程的解析解为 wx)=-2+y2 4 ■串行程序：jacobi.c http://math.ecnu.edu.cn/~jypan 8

http://math.ecnu.edu.cn/~jypan 8 程序示例 例：取  串行程序： jacobi.c 2 2 ( , ) 1, ( , ) 4 x y f xy gxy + = = − 此时 Poisson 方程的解析解为 2 2 (,) 4 x y uxy + = −

并行算法 ■并行求解的基本思想：区域分解 ●采用区域分解技术： 假设使用np个进程并行求解，则将整个求解区域分解成 npx x npy个子区域，其中npx×npy=np ●每个进程负责求解一个子区域 ●相邻两个子区域有一个网格步的重叠： 便于子区域间的数据传递 ●每个子区域包含的网格点大致相等 ●以3×3的区域分解为例 http://math.ecnu.edu.cn/~jypan 9

http://math.ecnu.edu.cn/~jypan 9 并行算法  并行求解的基本思想：区域分解  采用区域分解技术： 假设使用 np 个进程并行求解，则将整个求解区域分解成 npx × npy 个子区域，其中 npx × npy = np  每个进程负责求解一个子区域  相邻两个子区域有一个网格步的重叠： 便于子区域间的数据传递  每个子区域包含的网格点大致相等  以 3 × 3 的区域分解为例

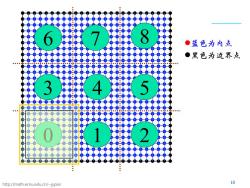
6 7 ●蓝色为内点 ●黑色为边界点 34】 0 12 http://math.ecnu.edu.cn/~jypan 10

http://math.ecnu.edu.cn/~jypan 10 蓝色为内点 黑色为边界点 0 1 2 3 4 5 6 7 8